二分查找
二分查找又叫折半查找,是在有序列表的基础上进行查找,每次查找可以筛掉一半的元素。
算法步骤
以升序数列$L[0…n-1]$为例,假设要查找的数为$x$:
让$x$与数列中间位置的元素$L[\lfloor \frac n2 \rfloor]$进行比较,如果相等则返回该元素下标,否则:
- 如果$x$比中间元素小,递归地对中间元素左边的数列(比二分查找小的元素)进行二分查找;
- 如果$x$比中间元素大,递归地对中间元素右边的数列(比二分查找大的元素)进行二分查找。
代码实现
Python实现
- 递归实现:
def BinarySearch(arr, target, left = 0, right = 0): """二分排序(递归实现) left=0,right=len(arr)-1""" if left == 0 and right == 0: right = len(arr)-1 if left > right or len(arr) == 0: return -1 mid = int((left + right) / 2) if target == arr[mid]: return mid elif target < arr[mid]: return BinarySearch(arr, target, left, mid-1) else: return BinarySearch(arr, target, mid+1, right) if __name__ == "__main__": arr = list(range(100)) target = 66 result = BinarySearch(arr, target) if result == -1: print(False) else: print(result) - 非递归实现:
def BinarySearch(arr, target): """二分排序(非递归实现)""" if len(arr) == 0: return -1 left = 0 right = len(arr)-1 while left <= right: mid = int((left + right) / 2) if target == arr[mid]: return mid elif target < arr[mid]: right = mid - 1 else: left = mid + 1 return -1 if __name__ == "__main__": arr = list(range(100)) target = 66 result = BinarySearch(arr, target) if result == -1: print(False) else: print(result)
C实现
- 递归实现:
#include <stdio.h> #define LEN 100 int BinarySearch(int arr[], int left, int right, int target) { if (left > right || arr == NULL) return -1; int mid = (left + right) / 2; if (target == arr[mid]) return mid; else if (target < arr[mid]) return BinarySearch(arr, left, mid-1, target); else return BinarySearch(arr, mid+1, right, target); } int main(void) { int arr[LEN]; for (int i = 0; i < LEN; i++) arr[i] = i; int target = 66; int result = BinarySearch(arr, 0, LEN-1, target); if (result == -1) printf("False\n"); else printf("%d\n", result); return 0; } - 非递归实现:
#include <stdio.h> #define LEN 100 int BinarySearch(int arr[], int left, int right, int target) { if (left > right || arr == NULL) return -1; while (left <= right) { int mid = (left + right) / 2; if (target == arr[mid]) return mid; else if (target < arr[mid]) right = mid - 1; else left = mid + 1; } return -1; } int main(void) { int arr[LEN]; for (int i = 0; i < LEN; i++) arr[i] = i; int target = 66; int result = BinarySearch(arr, 0, LEN-1, target); if (result == -1) printf("False\n"); else printf("%d\n", result); return 0; }
散列表查找
散列表查找又叫哈希表查找,是通过记录存储位置和关键字构建一个确定的关系$f$,使得每个关键字$key$对应一个存储位置$f(key)$,称这个为散列技术。其中,$f$称为散列函数或者哈希函数。
通过散列技术将记录存储在一块连续的存储空间中,这块连续的空间称为散列表或者哈希表。
散列表最适合查找与给定的值相等的记录。
散列函数的冲突:
在使用散列表的过程中,可能会有两个关键字通过散列函数得到的存储地址是一样的,这个现象被称为冲突。此时就需要通过冲突解决办法来解决冲突。在解决冲突的同时也要保证查找和插入效率问题。同时为了避免冲突,散列函数的构造也是很重要的。
算法步骤
散列函数的构造方法
选取散列函数的参考:
- 计算散列地址所需的时间;
- 关键字长度;
- 散列表大小;
- 关键字的分布情况;
- 查找记录的频率。
直接定址法
直接定址法就是直接通过取关键字的某个线性值作为散列地址:
$$ f(key)=a \cdot key+b\quad(a,b为常数) $$
例如,要存储0-100岁的人口统计表,就可以采用散列函数为:
f(key) = key
数字分析法
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布比较 均匀,就可以考虑这个方法。
Example:
假设某公司的员工登记表以员工的手机号作为关键字。手机号一共11位。前3位是接入号,对应不同运营商的子品牌;中间4位表示归属地;最后4位是用户号。不同手机号前7位相同的可能性很大,所以可以选择后4位作为散列地址,或者对后4位反转(1234 -> 4321)、循环右移(1234 -> 4123)、循环左移等等之后作为散列地址。
平方取中法
假设关键字是1234,平方之后是1522756,再抽取中间3位227,用作散列地址。平方取中法比较适合于不知道关键字的分布,而位数又不是很大的情况。
折叠法
将关键字从左到右分割成位数相等的几部分,最后一部分位数不够时可以短些,然后将这几部分叠加求和, 并按散列表表长,取后几位作为散列地址。
比如关键字是9876543210,散列表表长是3位,将其分为四组,然后叠加求和:987 + 654 + 321 + 0 = 1962,取后3位962作为散列地址。
折叠法事先不需要知道关键字的分布,适合关键字位数较多的情况。
除留取余数法
此方法为最常用的构造散列函数方法。
除留取余数法:
$$ f(key)=key\enspace mod\enspace p\quad (p\le m),\ m为散列表长 $$
这种方法不仅可以对关键字直接取模,也可在折叠、平方取中后再取模。根据经验,若散列表表长为$m$,通常$p$为小于或等于表长(最好接近$m$)的最小质数,可以更好的减小冲突。
随机数法
$$ f(key)=random(key),\quad random是随机函数 $$
当关键字的长度不等时,采用这个方法构造散列函数是比较合适的。
处理散列表冲突问题的方法
开放地址法
开放地址就是一旦发生冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并且记录它。有三种寻找空散列地址的方法:
-
线性探测法
$$ f’(key)=(f(key)+d)% n,\quad 其中d取(0,1,2,…,n-1),\ n为散列表的长度 $$
$d$初始为0,如果有冲突,那么$d$就通过递增来寻找空的散列地址。
Example:
下标 0 1 2 3 4 5 6 7 8 9 10 11 关键字 12 25 16 67 56 在如上所示的散列表中插入37。首先使用散列函数计算37的散列地址:$f’(37)=f(37)%12=1$(这里假设$f(key)=key$)。 而下标为1的位置已经存放了25,那就只能继续寻找下一个空散列地址:$f’(37)=(f(37)+1)%12=2$。
2这个位置没有内容,所以得到:
下标 0 1 2 3 4 5 6 7 8 9 10 11 关键字 12 25 37 16 67 56 使用线性探测来解决冲突问题,会造成冲突堆积。所谓的冲突堆积就是上例的37,它本来是属于下标1的元素,现在却占用了下标为2的空间。如果现在需要存放原本存放在下标为2的元素,就会再次发生冲突,这个冲突会一直传播下去,大大减低查找和插入效率。 -
二次探测法
$$ f’(key)=(f(key)+q^2)%n,\quad 其中q取(0,1,-1,2,-2,…,\frac n2,-\frac n2),\ n为散列表的长度 $$
二次探测法其实是对线性探测的一个优化,增加了平方可以不让关键字聚集在某一块区域。
Example:
下标 0 1 2 3 4 5 6 7 8 9 10 11 关键字 12 25 37 16 67 56 插入元素7,通过二次探测的散列函数计算得到:$f’(7)=f(7)%12=7$。 但下标为7的位置已经存放了67,所以需要寻找下一个存储地址:$f’(7)=(f(7)+1^2)%12=8$。
下标为8的位置已经存放了56,继续寻找: $f’(7)=(f(7)+(-1^2))%12=6$。
6这个位置为空,得到:
下标 0 1 2 3 4 5 6 7 8 9 10 11 关键字 12 25 37 16 7 67 56 -
随机探测法
$$ f’(key)=(f(key)+d)%m,\quad d为随机数,m为表长 $$
在实现中应预先用随机数发生器产生一个随机序列,将此序列作为依次探测的步长。这样就能使不同的关键字具有不同的探测次序,从而可以避免或减少堆积。
多重散列法
多重散列法又叫再散列函数法。其公式如下:
$$ f’(key)=RH(key) $$
其中$RH$就是不同的散列函数,这些散列函数可以是任何散列函数。只要其中一个发生了冲突,就马上换一个散列函数,直到冲突解决。缺点就是增加了很多计算时间。
链地址法
链地址法就是当冲突发生时,用链表来存放同义词(即存放在当前位置,每个位置使用链表存放同义词)。这个思路和图的邻接表存储方式很相似。
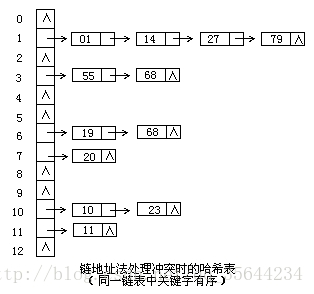
公共溢出区法
公共溢出区法就是把那些冲突的元素直接追加到另外一个溢出表中,如下图所示:

在查找的时候,如果在基本表没有找到,那么就只能去溢出表中进行顺序查找。这个方法比较适合冲突元素少的情况。
代码实现
Python实现
- 除留取余数法构造散列函数,开放地址法-线性探测处理散列表冲突:
class HashTable: def __init__(self, size): self.elem = [None for i in range(size)] self.size = size def hash(self, key): """除留取余数法构造哈希函数""" return key % self.size def insert_hash(self, key): address = self.hash(key) # 开放地址法-线性探测 while self.elem[address]: address = (address+1) % self.size self.elem[address] = key def search_hash(self, key): star = address = self.hash(key) while self.elem[address] != key: address = (address + 1) % self.size if not self.elem[address] or address == star: return -1 return address if __name__ == "__main__": list_a = [12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34] hash_table = HashTable(12) for i in list_a: hash_table.insert_hash(i) for i in hash_table.elem: if i: print((hash_table.elem.index(i), i), end=" ") print("") print(hash_table.search_hash(15)) print(hash_table.search_hash(33))


评论