数据库体系结构
数据描述有两种形式:
- 逻辑描述:指程序员或用户用以操作的数据形式,是抽象的概念化数据。
- 物理描述:指数据在存储设备上的存储方式,物理数据是实际存放在存储设备上的数据。
三级模式结构
实际上有许多不同的数据库产品,但它们的体系结构基本上都具有相同的特征,采用“三级模式和两级映像”:
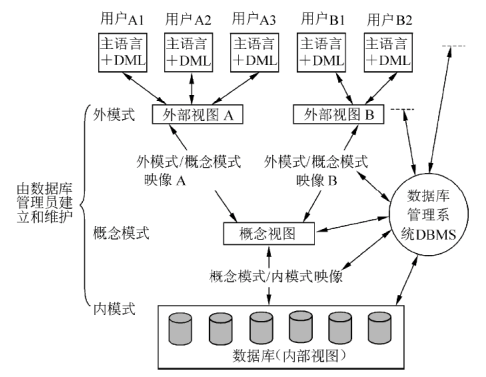
三级结构有3类数据模型:
- 外模型:用户使用的数据视图,是一种局部的逻辑数据视图,表示用户所理解的实体、实体属性和实体关系。
- 概念模型:全局的逻辑数据视图,是数据库管理员所看到的实体、实体属性和实体之间的联系。
- 内模型:数据的物理存储模型。
三个物理模型分别对应数据库系统的3层结构:
-
外模式(子模式、用户模式):数据库用户的数据视图,是与某一应用程序有关的数据的逻辑表示。
外模式用DBMS的外模式描述语言(外模式DDL)来定义。
-
概念模式(模式):所有用户的公共数据视图,与具体的应用程序和应用程序开发工具无关。
概念模式用DBMS的模式描述语言(模式DDL)来定义。
-
内模式(物理模式、存储模式):是数据在数据库内部的表示方式。
内模式由DBMS的内模式描述语言(内模式DDL)来描述,由设备介质语言来定义。
定义所有的内部记录类型、索引和文件的组织方式。
两级模式映象
数据库系统在三级模式之间提供了两级映像:
- 模式——内模式映像存在于概念级和内部级之间,实现概念模式和内模式间的相互转换。
- 外模式——模式映像:存在于外部级和概念级之间,实现了外模式和概念模式之间的相互转换。
数据的独立性(指数据与程序独立)是由DBMS的二级映像功能来保证的。数据的独立性包括:
-
物理独立性:指当数据库的内模式发生改变时,数据的逻辑结构不变。
物理独立性可以保证,当数据的物理结构改变时,应用程序不用改变。
但是,为了保证应用程序能够正确执行,需要修改概念模式和内模式之间的映像。
-
逻辑独立性:指用户的应用程序与数据库的逻辑结构是相互独立的。
数据的逻辑结构发生变化后,用户程序也可以不修改。
但是,为了保证应用程序能够正确执行,需要修改外模式和概念模式之间的映像。
数据模型
在数据库技术中,表示实体类型及实体类型间联系的模型称为数据模型。
数据模型有以下类型:
- 概念数据模型:从信息世界中抽象的数据模型;
- 结构数据模型:从计算机世界中抽象出的DBMS支持的数据模型。
概念数据模型
概念数据模型用于信息世界建模,一般采用实体-联系方法(E-R方法)。概念数据模型的常用术语有:
-
实体:客观存在并可以相互区别的事物称为实体。
如一个单位、一个职工、一个部门或一个项目等。
-
属性:描述实体的特性称为属性,一个实体可以由若干个属性来刻画。
属性的具体取值称为属性值,用以表示一个具体实体。
-
码:唯一标识实体的属性集称为码。
-
域:属性的取值范围称为该属性的域。
-
实体型:具有相同属性的实体必然具有共同的特征和性质,用实体名及其属性名集合来抽象和刻画同类实体,称为实体型。
例如,学生(学号,姓名,性别,班号)就是一个实体型。
-
实体集:同型实体的集合称为实体集。
例如,全体学生就是一个实体集。
-
联系:实体(型)之间的对应关系称为联系。联系分为两种:
- 实体内部各属性之间的联系;
- 实体之间的联系。
两个实体型之间的联系有3种类型:
- 一对一联系(1:1);
- 一对多联系(1:n);
- 多对多联系(m:n)。
实体-联系方法表示的概念数据模型称为E-R图。E-R图是抽象和描述现实世界的有力工具:
- 实体型:用矩形表示,矩形框内写明实体名;
- 属性:用椭圆形表示,并用无向边将其与相应的实体连接起来;
- 联系:用菱形表示,菱形框内写明联系名,并用无向边将其分别与有关实体连接起来,同时在无向边旁标上联系的类型。
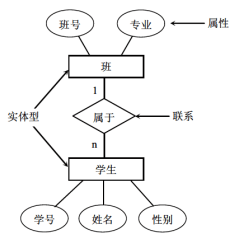
结构数据模型
结构数据模型是直接面向数据库的逻辑结构。这类模型涉及到计算机系统和数据库管理系统,所以称为结构数据模型。任何一个DBMS都以某个结构数据模型为基础,或者说支持某个结构数据模型。
常用术语:
-
数据项:又称字段,是数据库中可以命名的最小逻辑数据单位。可以是一个数或个字符串,用它描述属性的数据。
-
记录:是数据项的有序集,即一个记录是由若干个数据项或字段组成,用它描述实体。
一般来说,数据只有被组成记录的形式才有实际意义。
-
文件:文件是一个具有符号名的一组同类记录的集合。文件包含记录的结构和记录的值。
结构数据模型主要包括:层次、网状、关系和面向对象模型。
关系模型是一种用二维表格结构快表示实体以及实体之间联系的数据模型。每个二维表由行、列组成,又可称为关系,关系模式是对关系的描述。因此可以说,关系模型是由关系模式组成的集合。
目前大多数数据库管理系统都是关系型的。
关系模型
术语
有关关系模型的术语:
-
关系:一个关系就是一张二维表,每个关系有一个关系名
-
元组:表中的一行即为一个元组,对应存储文件中的一个记录值。
-
属性:表中的列称为属性,每一列有一个属性名。
属性值相当于记录中的数据项或者字段值。
-
域:属性的取值范围。
-
关系模式:对关系的描述称为关系模式,由关系名和其属性集合构成,关系模式的格式为:关系名(属性名1,属性名2,…,属性名n)
-
候选码(候选健):属性或属性组合其值能够唯一地标识一个元组。
-
主码(主键):在一个关系中可能有多个候选码,从中选择一个作为主码。
-
主属性:所有候选键都称为主属性,其他的属性都称为非码属性。
-
外码(或外键):如果一个关系中的属性或属性组并非该关系(二维表)的码,但它们是另外一个关系(二维表)的码,则称其为该关系的外码。
-
全码:关系模式的所有属性组是这个关系模式的候选码,称为全码。
-
超码(超键):一个包含码的属性集称为超码。
例如学号是码,则(学号,姓名)就是一个超码。
完整性约束
完整性规则保证用户对数据库做修改时不会破坏数据的一致性。
-
实体完整性(Entity Integrity,引用完整性):规定基本关系R的主属性A不能取空值。
即主属性不能为空。
-
参照完整性(Referential Integrity):若F是基本关系R的外码,它与基本关系S的主码Ks相对应(基本关系R和S不一定是不同的关系),则对于R中每个元组在F上的值可以取:
- 空值(F的每个属性值均为空值);
- S中某个元组的主码值。
即实体之间的关联可以变现为:关系R用外码F与关系S关联,外码F的值可以为空也可以为关系S中某个元组(记录)的主码值。
-
用户定义完整性(User Defined Integrity):针对某一具体的关系数据库的约束条件,反映某一具体应用所涉及的数据必须满足的语义要求,由应用的环境决定。
例如,银行的用户账户规定必须大于等于100000、小于999999。
关系代数运算符
关系操作的特点是操作对象和操作结果都是集合,而非关系数据模型的数据操作方式则为一次一个记录的方式。
关系数据语言分为三类:
- 关系代数语言;
- 关系演算语言;
- 具有关系代数和关系演算双重特点的语言。
关系演算语言包含:
- 元组关系演算语言;
- 域关系演算语言。
关系代数运算符有4类:
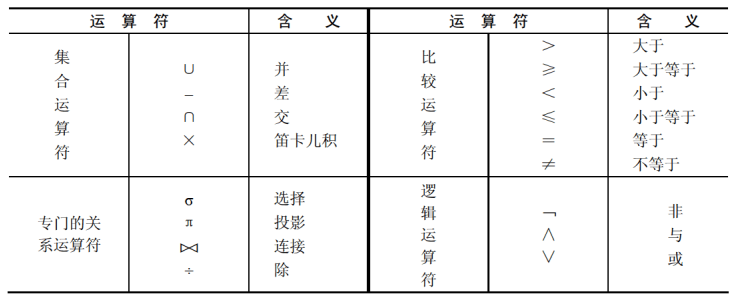
基本关系代数运算是对两个具有相同的关系模式的关系进行运算。关系$R$与$S$具有相同的关系模式,即$R$与$S$的元数相同(结构相同)。
基本关系代数运算包含:
-
并(Union):关系$R$与$S$的并是由属于$R$或属于$S$的元组构成的集合,记作$R \cup S$,其形式定义如下:
$$ R \cup S = \{ t | (t \in R) \vee (t \in S) \} $$
式中$t$为元组变量。
-
差(Difference):关系$R$与$S$的差是由属于$R$但不属于$S$的元组构成的集合,记作$R-S$,其形式定义如下:
$$ R-S = \{ t| (t \in R) \wedge (t \not\in S) \} $$
-
交(Intersection):关系$R$与$S$的交是由属于$R$同时又属于$S$的元组构成的集合,记作$R \cap S$,其形式定义如下:
$$ R \cap S = \{ t| (t \in R) \wedge (t \in S) \} $$
$R \cap S = R-(R-S)$,或者$R \cap S = S-(S-R)$。
扩展的关系代数运算可以从基本的关系运算中导出,包括:
-
广义笛卡儿积(Extended Cartesian Product):两个元组分别为$n$目和$m$目的关系$R$和$S$的广义笛卡儿积是一个$(n+m)$列的元组的集合。
元组的前$n$列是关系$R$的一个元组,后$m$列是关系$S$的一个元组,记作$R \times S$,其形式定义如下:
$$ R \times S = \{ t| (t \ = \ <t^n, t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \} $$
如果$R$和$S$中有相同的属性名,可在属性名前加关系名作为限定,以示区别。若$R$有$K_1$,个元组,$S$有$K_2$个元组,则$R$和$S$的广义笛卡儿积有$K_1 \times K2$个元组。
$<t^n, t^m>$是一个元组$t^n$和$t^m$拼接成的一个元组。
-
投影(Projection):投影运算是从关系的垂直方向进行运算,在关系$R$中选出若干属性列$A$组成新的关系,记作$\pi_A (R)$,其形式定义如下:
$$ \pi_A (R) = \{ t[A]|t \in R \} $$
-
选择(Selection):选择运算是从关系的水平方向进行运算,是从关系$R$中选择满足给定条件的诸元组,记作$\sigma_F (R)$其形式定义如下:
$$ \sigma_A (R) = \{ t| (t \in R) \wedge F(t) = True \} $$
其中,$F(t)$中的运算对象可以是:
- 属性名(或列的序号);
- 常数;
- 运算符;
- 算术比较符($<, \le, >, \ge, \neq$);
- 逻辑运算符($\wedge, \vee, \neg$)。
-
连接(Join):连接运算是从两个关系$R$和$S$的笛卡儿积中选取满足条件的元组。
可以认为笛卡儿积是无条件连接,其他的连接操作认为是有条件连接。
-
$\theta$连接:从$R$与$S$的笛卡儿积中选取属性间满足一定条件的元组。记作:
$$ R \mathop{\Join}\limits_{X \theta Y} S = \{ t| (t=<t^n,t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (t^n[X] \ \theta \ t^m[Y]) \} $$
其中:
- $X \theta Y$:连接的条件;
- $\theta$:比较运算符;
- $X$和$Y$分别为$R$和$S$上度数相等且可比的属性组;
- $t^n\left[ X \right]$表示$R$中$t^n$元组的对应于属性$X$的一个分量;
- $t^m[Y]$表示$S$中$t^m$元组的对应于属性$Y$的一个分量。
$\theta$连接也可以表示为:
$$ R \mathop{\Join}\limits_{i \theta j} S = \{ t| (t=<t^n,t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (t^n[i] \ \theta \ t^m[j]) \} $$
其中,
-
$i=1,2,3,\cdots,n$;
-
$j=1,2,3,\cdots,m$;
-
$i \theta j$:
从两个关系$R$和$S$中选取$R$的第$i$列和$S$的第$j$列之间满足$\theta$运算的元组进行连接。
$\theta$连接可以由基本的关系运算笛卡儿积和选取运算导出。因此,$\theta$连接可表示为:
$$ R \mathop{\Join}\limits_{X \theta Y} S = \sigma_{X \theta Y}(R \times S) $$
或:
$$ R \mathop{\Join}\limits_{i \theta j} S = \sigma_{i \theta j}(R \times S) $$
-
等值连接:当$\theta$为“=”时,称之为等值连接,记为$R \mathop{\Join}\limits_{i = j} S$,其形式定义如下:
$$ R \mathop{\Join}\limits_{i = j} S = \{ t| (t=<t^n,t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (t^n[i] = t^m[j]) \} $$
-
$F$连接:从关系$R$和$S$的笛卡尔积中选取属性值满足某一公式$F$的元组,记为$\mathop{\Join}\limits_{F}$。
$F$是形为$F_1 \wedge F_2 \wedge \cdots \wedge F_n$的公式,每个$F_p$是形为$i \theta j$的式子。
-
自然连接:自然连接是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且在结果集中将重复属性列去掉。
若:
-
$t^n \in R$,$t^m \in S$;
-
$R$和$S$具有相同的属性组$B$,且$B=(B_1,B_2,,B_k)$;
-
假定$R$关系的属性:
$$ A_1,A_2,\cdots,A_{n-k},B_1,B_2,\cdots,B_k $$
-
$S$关系的属性:
$$ B_1,B2,\cdots,B_k,B_{k+1},B_{k+2},\cdots,B_m $$
自然连接可以记为$R \Join S$,其形式定义如下:
$$ R \Join S = \{ t| (t = <t^n, t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (R.B_1 = S.B_1) \wedge (R.B_2 = S.B_2) \wedge \cdots \wedge (R.B_k = S.B_k) \} $$
一般连接是从关系的水平方向运算,而自然连接不仅要从关系的水平方向运算,而且要从关系的垂直方向运算(去掉重复属性)。
-
-
-
外连接(Outer Jion):外连接运算是连接运算的扩展,可以处理由于连接运算而缺失的信息。
外连接运算有3种:
-
左外连接(Left Outer Jion,⟕):取出左侧关系中所有与右侧关系中任一元组都不匹配的元组,用空值$null$充填所有来自右侧关系的属性,构成新的元组,将其加入自然连接的结果中。
-
右外连接(Right Outer Jion,⟖):取出右侧关系中所有与左侧关系中任一元组都不匹配的元组,用空值$null$填充所有来自左侧关系的属性,构成新的元组,将其加入自然连接的结果中。
-
全外连接(Full Outer Jion,⟗)。完成左外连接和右外连接的操作。即填充左侧关系中所有与右侧关系中任一元组都不匹配的元组,并填充右侧关系中所有与左侧关系中任一元组都不匹配的元组,将产生的新元组加入自然连接的结果中。

-
-
除(Division):给定关系$R(X,Y)$和$S(Y,Z)$,$X、Y、Z$为属性组。$R \div S$应当满足元组在$X$上的分量值$x$的象集$Y_x$包含关系$S$在属性组$Y$上投影的集合。其形式定义如下:
$$ R \div S = \{ t^n[X] | (t^n \in R) \wedge (\pi_y (S) \subseteq Y_x) \} $$
其中,$Y_x$为$x$在$R$中的象集,$x=t^n[X]$,且$R \div S$的结果集的属性组为$X$。
除运算是同时从关系的水平方向和垂直方向进行运算。
SQL 语句
SQL(Structured Query Language,发音为 sequal)是一种专门用来与数据库沟通的语言。通过 SQL,用户可以对数据库进行各种操作。
标准 SQL 由 ANSI 标准委员会管理,从而称为 ANSISQL。
查看更多 SQL语句 相关内容。
分类
-
DDL(Data Definition Language,数据定义语言):用来定义数据库对象:数据库,表,列等。
关键字:
CREATE、DROP、ALTER等。 -
DML(Data Manipulation Language,数据操作语言):用来对数据库中表的数据进行增删改。
关键字:
INSERT、DELETE、UPDATE等。 -
DQL(Data Query Language,数据查询语言):用来查询数据库中表的记录。
关键字:
SELECT等。 -
DCL(Data Control Language,数据控制语言):用来定义数据库的访问权限和安全级别,及创建用户。
数据定义语言(DDL)
CREATE——创建:
-
建立数据库:
CREATE DATABASE 数据库名; -
建立基本表:
CREATE TABLE tab_name ( 列名 数据类型 [列级完整性约束条件], ... 表级完整性约束条件, ... );完整性约束有3种子句:
PRIMARY KEY:主键约束;CHECK:检查约束;FOREIGN KEY:外键约束;NOT NULL:非空约束;UNIQUE:唯一约束;DEFAULT:默认约束。
定义列时使用的基本数据类型如下:
NTEGER:整数(也可写成INT)。FLOAT(n):浮点数,精度至少为n位数字。NUMERIC(p,d):定点数,由p位数字(不包括符号、小数点)组成,小数点后面有d位数字(也可写成DECIMAL(p,d)或DEC(p,d))。CHAR(n):长度为n的定长字符串。DATETIME:日期时间型。
ALTER TABLE——修改表结构:
-
增加新列:
ALTER TABLE 表名 ADD 列名 类型 -
修改列的定义:
ALTER TABLE 表名 ALTER COLUMN 列名 新类型 -
删除列:
ALTER TABLE 表名 DROP COLUMN 列名
DROP TABLE——删除基本表:
DROP TABLE 表名
数据操纵语言(DML)
INSERT INTO——插入:
-
直接插入元组值:
INSERT INTO 表名(列名序列)VALUES (元组值)或者:
INSERT INTO 表名 (列名 序列) (TABLE (元组值), (元组值), ...) -
插入一个查询的结果值:
INSERT INTO 表名 (列名序列) SELECT 查询语句
DELETE FROM——删除:
DELETE FROM 表名 [WHERE 条件表达式]
UPDATE——修改:
UPDATE 表名
SET 列名=值表达式[, 列名=值表达式...]
[WHERE条件表达式]
数据查询语言(DQL)
SELECT——查询:
SELECT 目标表的列名或列表达式序列
FROM 关系名表序列
[WHERE 行条件表达式]
[GROUP BY 列名序列
[HAVING 组条件表达式]]
[ORDER BY 列名[ASC|DESC]...]
WHERE 条件查询
SELECT 目标表的列名或列表达式序列
FROM 关系名表序列
WHERE 行条件表达式
运算符:
| 运算符 | 说明 | 运算符 | 说明 |
|---|---|---|---|
= |
等于 | > |
大于 |
<> 或 != |
不等于 | >= |
大于等于 |
< |
小于 | !> |
不大于 |
<= |
小于等于 | BETWEEN |
范围在指定的两个值之间 |
!< |
不小于 | IS NULL |
为 NULL 的值 |
IS NOT NULL |
不为 NULL 的值 | AND |
逻辑与 |
OR |
逻辑或 | NOT逻辑非 |
|
IN |
匹配包含在集合中的值 | NOT IN |
指定不包含在集合中的值 |
LIKE |
字符模糊配对 |
LIKE字符模糊配对包含以下通配符:
SELECT 目标表的列名或列表达式序列
FROM 关系名表序列
WHRER 列名 LIKE '_ABC%';
%:表示任何字符出现任意次数。_:表示匹配单个任意字符。
ORDER BY 排序数据
ORDER BY可以指定多个列来排序,排序规则有:
| 关键字 | 规则说明 |
|---|---|
ASC |
升序排序 |
DESC |
降序排序 |
SELECT 目标表的列名或列表达式序列
FROM 关系名表序列
[...]
[ORDER BY 列名 [ASC|DESC] ...]
ORDER BY子句必须是SELECT命令中的最后一个子句。
GROUP BY 分组数据
SELECT 目标表的列名或列表达式序列
FROM 关系名表序列
[GROUP BY 列名序列
[HAVING 组条件表达式]]
HAVING是GROUP BY的分组条件控制语句。HAVING的操作符和WHERE相同。- 被
WHERE过滤掉的记录并不会出现在分组中。
聚合函数
聚合函数实现数据统计等功能。
函数名|功能
AVG|计算一个数值型表达式的平均值
COUNT|计算指定表达式中选择的项数,COUNT(*)统计查询输出的行数
MIN|计算指定表达式中的最小值
MAX|计算指定表达式中的最大值
SUM|计算指定表达式中的数值总和
STDEV|计算指定表达式中所有数据的标准差
STDEVP|计算总体标准差
SELECT 目标表的列名或列表达式序列
FROM 关系名表序列
WHERE 使用了聚合函数的条件判断
[ ... ]
或:
SELECT 聚合函数
FROM 关系名表序列
聚合函数可以使用算数运算符。
聚合函数常与
GROUP BY子句一起使用。
连接
| 连接符号 | 说明 |
|---|---|
INNER JOIN |
内连接(默认)。 内连接又包括等值连接、非等值连接和自连接。 |
OUTER JOIN |
外连接。 又包括: LEFT OUTER JOIN(左外连接);RIGHT OUTER JOIN(右外连接);FULL OUTER JOIN(全外连接) |
子查询
子查询是指将SELECT作为其它语句的子句使用。例如在WHERE、FROM中使用SELECT。
数据控制语言(DCL)
数据控制控制的是用户对数据的存储访问权力,是由DBA决定的。但是,某个用户对某类数据具有何种权利,是个政策问题而不是技术问题。
授权语句格式(GRANT):
GRANT <权限>[, <权限>] ...
[ON <对象类型> <对象名>]
TO<用户>[, <用户>]...
[WITH GRANT OPTION];
不同类型的操作对象有不同的操作权限,常见的操作权限如下:
| 对象 | 对象类型 | 操作权限 |
|---|---|---|
| 属性列 | TABLE |
SELECT、INSERT、UPDATE、DELETE、ALL PRIVILEGES |
| 视图 | TABLE |
SELECT、INSERT、UPDATE、DELETE、ALL PRIVILEGES |
| 基本表 | TABLE |
SELECT、INSERT、UPDATE、DELETE、ALTER、INDEX、ALL PRIVILEGES |
| 数据库 | DATABASE |
CREATETAB |
- 建立表的权限,可由DBA授予普通用户;
WITH GRANT OPTION:表示获得了这些权限的用户还可以将权限赋给其他用户。
收回权限语句格式(REVOKE):
REVOKE <权限>[, <权限>]...
[ON <对象类型> <对象名>]
FROM <用户>[, <用户>];
视图
视图是从一个或者多个基本表或视图中导出的虚拟表。
创建视图:
CREATE VIEW 视图名 (列表名) AS
SELECT 查询子句
[WITH CHECK OPTION];
- 子查询可以是任意复杂的
SELECT语句,但通常不允许含有ORDER BY子句和DISTINCT短语。 WITH CHECK OPTION:表示对UPDATE、INSERT、DELETE操作时保证更新、插入或删除的行满足视图定义中的谓词条件(即子查询中的条件表达式)。- 组成视图的属性列名或者全部省略或者全部指定。如果省略属性列名,则隐含该视图由
SELECT子查询目标列的主属性组成。 - 对视图进行的增改操作实际上是对基本表进行操作。
删除视图:
DROP VIEW 视图名;
索引
数据库中的索引是某个表中一列或者若干列值的集合和相应的指向表中物理标识这些值的数据页的逻辑指针清单。
索引分为:
- 聚集索引:指索引表中索引项的顺序与表中记录的物理顺序一致的索引;
- 非聚集索引。
对数据库表创建和删除索引,修改的是数据库的内模式。
关系数据库的规范化
关系模式
一个关系模式应当是一个五元组(含关系名):$R<U,D,dom,F>$。
其中:
- $R$:关系名,是符号化的元祖语义;
- $U$:一组属性名;
- $D$:属性组$U$中的属性来自域$D$;
- $dom$:属性到域的映射;
- $F$:属性组$U$上的一组数据依赖(函数依赖)。
$D$和$dom$对模式设计关系不大,通常将关系模式看作是一个三元组:$R<U,F>$。
当且仅当$U$上的一个关系$r$满足$F$时,称$r$为关系模式$R<U,F>$的一个关系。
函数依赖
数据依赖是通过一个关系中属性间值的相等与否体现出来的数据间的相互关系。
-
函数依赖:设$R(U)$是属性集U上的关系模式,$X$、$Y$是$U$的子集。若对$R(U)$的任何一个可能的关系$r$,$r$中不可能存在两个元组在$X$上的属性值相等,而在$Y$上的属性值不等(即,在关系$r$中,元组在$X$上的属性值相等,那么在$Y$上的属性值也相等),则称X函数决定Y或Y函数依赖于X,记作$X \rightarrow Y$。
如,学生表中,$学号 \rightarrow 姓名$。
属性之间有3种关系,但并不是每一种都存在函数依赖。如果$X$和$Y$之间的对应关系是:
- $1-1$:存在函数依赖$X \rightarrow Y$和$Y \rightarrow Y$;
- $n:1$:存在函数依赖$X \rightarrow Y$;
- $n:m$:不存在函数依赖。
-
非平凡的函数依赖:$X \rightarrow Y$,但$Y \not\subseteq X$,则称$X \rightarrow Y$是非平凡的函数依赖。
例如,$姓名 \not\subseteq 学号$,则$学号 \rightarrow 姓名$是一个非平凡的函数依赖。
-
平凡的函数依赖:如果$X \rightarrow Y$,但$Y \subseteq X$,则称$X \rightarrow Y$是平凡的函数依赖。
例如,$学号 \subset (学号,课程号)$,则$(学号,课程号) \rightarrow 学号$是一个平凡的函数依赖。
-
完全函数依赖:在R(U)中,如果$X \rightarrow Y$,并且对于X的任何一个真子集$X’$都有**$X’$不能决定$Y$**,则称$Y$对$X$完全函数依赖,记作$X \stackrel{f}{\longrightarrow} Y$。
即需要由$X$的所有属性才能决定$Y$的,才能称为完全函数依赖。
如,$(学号,课程号) \rightarrow 成绩$。
如果$X$仅包含一个属性,那么此时必为完全函数依赖。
-
部分函数依赖:如果$X \rightarrow Y$,但Y不完全函数依赖于X,则称Y对X部分函数依赖,记作$X \stackrel{P}{\longrightarrow} Y$。部分函数依赖也称为局部函数依赖。
如,(学号,班级代号) $\rightarrow$ 姓名,因为学号 $\rightarrow$ 姓名,所以(学号,班级代号) $\stackrel{P}{\longrightarrow}$ 姓名。
-
传递依赖:在$R(U,F)$中(F是U上的一组函数依赖),如果$X \rightarrow Y,\ Y \not\subseteq X,\ Y \rightarrow Z$,则称Z对X传递依赖($X \rightarrow Z$)。
即$X \stackrel{f}{\longrightarrow} Y$,且$Y \rightarrow Z$,则$X \rightarrow Z$。
-
码:设$K$为$R(U,F)$中属性的组合,若$K \rightarrow U$,且对于$K$的任何一个真子集$K’$都有$K’$不能决定$U$,则$K$为$R$的候选码。
即$K \stackrel{f}{\rightarrow} U$,那么K是R的候选码。
若有多个候选码,则选一个作为主码(主键,主关键字)。候选码通常也称为候选关键字(候选键,键)。
-
主属性和非主属性:包含在任何一个候选码中的属性称为主属性,否则称为非主属性。
-
外码:若$R(U)$中的属性或属性组$X$非$R$的码,但$X$是另一个关系的码,则称$X$为外码。
函数依赖的公理系统(Armstrong公理系统):
设关系模式$R(U,F)$,其中$U$为属性集,$F是$U$上的一组函数依赖,那么有以下推理规则:
-
自反律(A1):若$Y \subseteq X \subseteq U$,则$X \rightarrow Y$为$F$所蕴涵(蕴含)。
如,(学号,姓名) $\rightarrow$ 姓名是函数依赖所蕴涵的。
-
增广律(A2):若$X \rightarrow Y$为F所蕴涵,且$Z \subseteq U$,则$XZ \rightarrow YZ$为$F$所蕴涵。
如,学号 $\rightarrow$ 姓名,班级 $\subseteq$ 学生表,那么(学号,班级) $\rightarrow$ (姓名,班级)是函数依赖所蕴涵的。
-
传递律(A3):若$X \rightarrow Y,\ Y \rightarrow Z$为$F$所蕴涵,则$X \rightarrow Z$为$F$所蕴涵。
根据上述3条推理规则又可推出下述3条推理规则:
- 合并规则:若$X \rightarrow Y,\ X \rightarrow Z$,则$X \rightarrow YZ$为F所蕴涵。
- 伪传递律:若$X \rightarrow Y,\ WY \rightarrow Z$,则$XW \rightarrow Z$为F所蕴涵。
- 分解规则:若$X \rightarrow Y,\ Z \subseteq Y$,则$X \rightarrow Z$为F所蕴涵。
合并规则和分解规则是两个互逆的规则。即$X \rightarrow Y,\ X \rightarrow Z$,可得$X \rightarrow YZ$;那么$X \rightarrow YZ$,也可得$X \rightarrow Y,\ X \rightarrow Z$(因为$Y,Z \sub YZ$)。
总结:
| 名称 | 条件 | 结论 |
|---|---|---|
| 函数依赖 | 元组在$X$上的属性值相等,那么在$Y$上的属性值也相等 | $X$函数决定$Y$或$Y$函数依赖于$X$,记作$X \rightarrow Y$ |
| 非平凡的函数依赖 | $X \rightarrow Y$,$Y \not\subseteq X$ | $X \rightarrow Y$是非平凡的函数依赖 |
| 平凡的函数依赖 | $X \rightarrow Y$,$Y \subseteq X$ | $X \rightarrow Y$是平凡的函数依赖 |
| 完全函数依赖 | $X \rightarrow Y$,$X’ \subset X$,$X’ \not\rightarrow Y$ | $Y$对$X$完全函数依赖,记作$X \stackrel{f}{\longrightarrow} Y$ |
| 部分函数依赖(局部函数依赖) | $X \rightarrow Y$,$X \stackrel{f}{\not\longrightarrow} Y$ | $Y$对$X$部分函数依赖,记作$X \stackrel{P}{\longrightarrow} Y$ |
| 传递依赖 | $X \rightarrow Y$,$Y \not\subseteq X$,$Y \rightarrow Z$ | $Z$对$X$传递依赖 |
| 名称 | 定义 |
|---|---|
| 码(候选码,候选关键字) | 若$K \stackrel{f}{\rightarrow} U$,则$K$为$R$的候选码 |
| 主属性 | 包含在任何一个候选码中的属性 |
| 非主属性 | 不包含在任何一个候选码中的属性 |
| 外码 | $X$非$R$的码,但$X$是另一个关系的码,则称$X$为外码 |
Armstrong公理系统:
| 定律 | 条件 | F蕴含 |
|---|---|---|
| 自反律 | $Y \subseteq X \subseteq U$ | $X \rightarrow Y$ |
| 增广律 | $X \rightarrow Y$,$Z \subseteq U$ | $XZ \rightarrow XZ$ |
| 传递律 | $X \rightarrow Y,\ Y \rightarrow Z$ | $X \rightarrow Z$ |
| 规则 | 条件 | F蕴含 |
|---|---|---|
| 合并规则 | $X \rightarrow Y,\ X \rightarrow Z$ | $X \rightarrow YZ$ |
| 伪传递律 | $X \rightarrow Y,\ WY \rightarrow Z$ | $XW \rightarrow Z$ |
| 分解规则 | $X \rightarrow Y,\ Z \subseteq Y$ | $X \rightarrow Z$ |
闭包计算
设关系模式$R<U,F>$,其中$U$为属性集,$F$是$U$上的一组函数依赖。称所有用Armstrong公理从F推出的函数依赖$X \rightarrow A_i$中,$A_i(X,A_i \subseteq U)$的属性集合为$X$的属性闭包,记为$X^{+}_{F}$或$X^{+}$。
定理:
设关系模式$R<U,F>$,其中$F$为函数依赖集,$X,Y \subseteq U$,则从$F$推出$X \rightarrow Y$的充要条件是$Y \subseteq X^{+}$。
属性的闭包计算用于求主键。
例如,给定关系$R(U,F)$,其中$U={A,B,C,D,E,H}$,$F={A \rightarrow B, B \rightarrow DH, A \rightarrow H, C \rightarrow E }$。
先根据$F$选取仅在$\rightarrow$左边出现的属性集(例如,$A$、$C$和$AC$)。根据选取的属性集进行闭包运算(先对$A$进行运算):
$$ (A)^{+} \rightarrow (A \ BH)^{+} \rightarrow (AB \ D \ H)^{+} \rightarrow (ABDH) $$
此时,$(ABDH)^{+}$无论再怎么推,结果都是$(ABDH)$,说明对$A$的闭包计算已经结束了,结果就是$(ABDH)$。
而$(ABDH) \neq U$,说明$A$并不是关系$R$的主键。
而对于$C$的函数依赖仅有$C \rightarrow E$,所以此时应该对$(AC)$进行闭包运算:
$$ (AC)^{+} \rightarrow (ABDH \ CE)^{+} \rightarrow (ABCDEH) $$
此时对$(AC)$的闭包计算结果$(ABCDEH) = U$,说明$(AC)$是关系$R$的主键。
关系模式的分解
对存在数据冗余、插入异常、删除异常问题的关系模式,应采取将一个关系模式分解为多个关系模式的方法进行处理(原来存储在一个二维表内的数据就要分散到多个二维表中)。要求是分解后的二维表不能丢失分解前二维表的信息。
为使分解后的模式保持原模式所满足的特性,其基本要求是模式分解具有:
- 无损连接性;
- 保持函数依赖性。
无损连接
无损连接性指的是对关系模式分解时,原关系模式下,任一合法的关系实例,在分解之后应能通过自然连接运算恢复起来。
设$\rho = \{ R_1<U_1,F_1>,\ R_2<U_2,F_2>,\ \cdots,\ R_k<U_k,F_k> \}$是关系模式$R<U,F>$的一个分解,如果对于$R$的任一满足$F$的关系$r$都有:
$$ r = \pi_{R1}(r) \Join \pi_{R2}(r) \Join \cdots \Join \pi_{Rk}(r) $$
则称这个分解$\rho$是满足依赖集$F$的无损连接。
$\pi()$运算是投影运算。
$\Join$运算是自然连接运算。
个人理解:
无损连接性就是指,关系模式拆分后(分成若干个小的关系模式,即$\rho$),$\rho$中的关系模式从总体上看,保持着与$R$一致的连接。$\rho$中的关系模式通过自然连接保持着原本的关系模式。重要的是$rho$中的关系模式可以通过自然连接恢复到原关系模式。
验证无损连接的充要条件:
如果$R$的分解为$\rho = \{R_1,R_2\}$,$F$为$R$所满足的函数依赖集合,则分解$\rho$具有无损连接性的充分必要条件为:
$$ R_1 \cap R_2 \rightarrow (R_1 - R_2) \\ 或 \\ R_1 \cap R_2 \rightarrow (R_2 - R_1) $$
无损连接的判定算法:
-
构造一个$k$行$n$列的表:
- 每一列对应一个属性$A_j$;
- 每一行对应分解$rho$中的一个关系模式$R_i<U_i, F_i>$。
若属性$A_j$属于$U_i$,则在第$i$行第$j$列上放符号$a_j$,否则放符号$b_{ij}$。
-
逐个检查$F$中的每一个函数依赖$FD_i$,并修改表中的元素:
取$F$中一个函数依赖$X_i \rightarrow A_j$($X_i$要属于$rho$中的任一关系),考虑这些行中第$j$列元素:
- 若其中有$a_j$,则全部改为$a_j$;
- 否则全部改为$b_{mj}$,$m$为这些行的行号最小值。
若某一行变成了$(a_1, a_2, \cdots, a_n)$,则分解$rho$具有无损连接性,算法终止。
-
比较扫描前后,表有无变化。
- 如有变化,则返回第2步;
- 否则算法终止,分解$rho$是有损连接。
例如,关系模式$R<U,F>$,其中,$U = \{ A, B, C \}$,$F = \{ A \rightarrow B, C \rightarrow B \}$。
判断$\rho = \{ AC, BC \}$是否具有无损连接性:
-
构造初始表:
$R_i$ $A$ $B$ $C$ AC $a_1$ $b_{12}$ $a_3 BC $b_{21}$ $a_2$ $a_3$ -
考察$A \rightarrow B$,将$AC$行的$B$列改为$a_2$:
$R_i$ $A$ $B$ $C$ AC $a_1$ $a_2$ $a_3 BC $b_{21}$ $a_2$ $a_3$ -
从上表中看出$AC$行为${a_1, a_2, a_3}$,所以判断该关系模式具有无损连接性。
保持函数依赖
设有关系模式$R$,$F$是$R$的函数依赖集,$Z$是$R$的一个属性集合,则称$Z$所涉及到的$F^+$中所有函数依赖为$F$在$Z$上的投影,即为$\pi_Z(F)$,有:
$$ \pi_Z(F) = \{ x \rightarrow y | (x \rightarrow y) \in F^+ 且 xy \subseteq z \} $$
设关系模式$R$的一个分解$\rho = \{ R_1<U_1,F_1>,\ R_2<U_2,F_2>,\ \cdots,\ R_k<U_k,F_k> \}$,$F$是$R$的依赖集,如果$F$等价于$\pi_{R1}(F) \cup \pi_{R2}(F) \cup \cdots \cup \pi_{Rk}(F)$,则称分解$\rho$具有依赖保持性。
该定义中的"等价"并不代表相等,而是$F$中所包含的函数依赖在分解的函数依赖中也被包含,或者在分解的函数依赖中能被推出。
- 一个无损连接分解不一定具有依赖保持性;
- 一个依赖保持性分解不一定具有无损连接性。
范式
关系数据库中的关系必须满足一定的规范化要求,对于不同的规范化程度可用范式来衡量。
范式是符合某一种级别的关系模式的集合,是衡量关系模式规范化程度的标准,达到范式的关系才是规范化的。
一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式的集合,这个过程称为规范化。
主要有6种范式,高一级范式是在低一级范式的基础上进一步满足一些要求,按要求从低到高分为:
-
第一范式(1NF):若关系模式R的每一个分量是不可再分的数据项,则关系模式R属于第一范式。
如,关系模式$R<U,F>$:
$$ U = \{ 学号,姓名,学院,院长,课程号,课程名,成绩 \} \\ F = \{ 学号 \rightarrow 姓名,学号 \rightarrow 学院,学院 \rightarrow 院长,课程号 \rightarrow 课程名,(学号,课程号) \rightarrow 成绩 \} $$
1NF可能存在的问题:
-
数据冗余:数据的冗余度大,R中可能出现多个元组在多个属性集中值相同;
-
修改异常:引起修改操作的不一致性,修改一条记录可能需要修改其他多条记录才能保持数据一致性(由数据冗余引起);
-
插入异常:主码不能取空值或部分空值,会出现插入异常;
-
删除异常:本该删除但又客观存在的元组,会出现删除异常。
即,删除掉的数据可能包含着其他本不该被删除的属性。
问题的原因是1NF中可能存在部分函数依赖。
-
-
第二范式(2NF):若关系模式$R \in 1NF$,且每一个非主属性完全依赖于码,则关系模式$R \in 2NF$。
即当1NF消除了对主键的部分函数依赖后就能满足2NF。
例如,$学号 \rightarrow 学院$,即$(学号,课程号) \stackrel{P}{\rightarrow} 学院$(部分依赖于码),所以$R \not\in 2NF$。
模式的分解需要保持函数依赖。根据$F$,将$R$分解为:
-
$R_1<U_1,F_1>$:
$$ U_1 = \{ 学号,姓名,学院,院长 \} \\ F_1 = \{ 学号 \rightarrow 姓名,学号 \rightarrow 学院,学院 \rightarrow 院长 \} $$
-
$R_2<U_2,F_2>$:
$$ U_2 = \{ 课程号,课程名 \} \\ F_2 = \{ 课程号 \rightarrow 课程名 \} $$
-
$R_3<U_3,F_3>$:
$$ U_3 = \{ 学号,课程号,成绩 \} \\ F_3 = \{ (学号,课程号) \rightarrow 成绩 \}
则,$R1 \in 2NF$,$R2 \in 2NF$,$R3 \in 2NF$。
2NF可能依然会存在数据冗余、修改异常、插入异常删除异常等问题。
-
-
第三范式(3NF):若关系模式$R(R \in 2NF)$中任何一个非主属性都不传递函数依赖于码。
若关系模式$R<U,F>$($U$为关系集,$F$为函数依赖集)中不存在这样的码$X$,使得:
- $X \rightarrow Y(Y \not\rightarrow X)$,
- $Y \rightarrow Z$,
则关系模式$R \in 3NF$,其中:
- $Y$为属性组,
- $Z(Z \not\subseteq Y)$为非主属性。
即当2NF消除了非主属性对主键的传递函数依赖,则称为3NF。
如,$R_1$中有$学号 \rightarrow 学院$,$学院 \rightarrow 院长$(非主属性"院长"传递依赖于主键"学号")。可将$R_1$分解为:
-
$R_{11}<U_{11},F_{11}>$:
$$ U_{11} = \{ 学号,姓名,学院 \} \\ F_{11} = \{ 学号 \rightarrow 姓名, 学号 \rightarrow 学院 \} $$
-
$R_{12}<U_{12},F_{12}>$:
$$ U_{12} = \{ 学院,院长 \} \\ F_{12} = \{ 学院 \rightarrow 院长 \} $$
-
BC范式(BCNF):关系模式$R<U,F>$属于BCNF($R$首先得满足3NF),当且仅当其$F$中每个依赖的决定因素必定包含R的某个候选码。
由BCNF的定义可以得到结论,一个满足BCNF的关系模式有:
-
满足3NF。
-
所有非主属性对每一个码都是完全函数依赖。
$$ 码 \stackrel{f}{\longrightarrow} 非主属性 $$
-
所有的主属性对每一个不包含它的码,也是完全函数依赖。
-
没有任何属性完全函数依赖于非码的任何一组属性。
一个满足BCNF的关系模式R己消除了插入和删除异常。
-
-
第四范式(4NF):
多值依赖:
给定的关系模式$R(U,F)$:
- $X,Y,Z \subseteq U$,
- $Z=U-X-Y$($Z$是$X \cup Y$的差集)。
当且仅当对$R$的任一关系$r$,给定的一对$(x,z)$值,有一组$Y$的值,这组值仅仅决定于$x$值而与$z$值无关。则关系模式$R$中的多值依赖$X \rightarrow\rightarrow Y$成立。
平凡的多值依赖:
- $X \rightarrow\rightarrow Y$成立,
- $Z = \Phi$,
则$X \rightarrow\rightarrow Y$为平凡的多值依赖。
例如,课程$\rightarrow\rightarrow$任课老师,课程$\rightarrow\rightarrow$参考书。
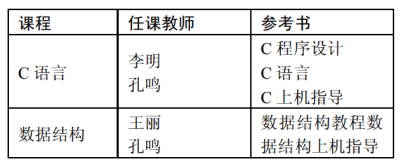
4NF定义:
设有一关系模式$R(U,F)$是1NF,如果对于$R$的每个非平凡多值依赖$X \rightarrow\rightarrow Y(Y \not\subseteq X)$,$X$都包含了$R$的一个候选码,则称$R$是第四范式,记为4NF。
例如,课程$\rightarrow\rightarrow$任课老师,课程$\rightarrow\rightarrow$参考书都是非平凡多值依赖,而课程不是码,所以不属于4NF。
-
第五范式(5NF)。
范式之间的关系:
$$ 5NF \sub 4NF \sub BCNF \sub 3NF \sub 2NF \sub 1NF $$
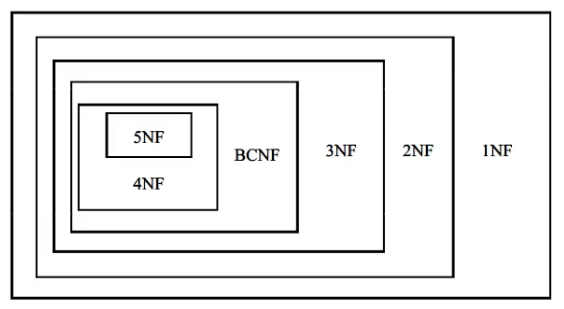
3NF和BCNE它们是进行规范化的主要目标。
1NF到4NF之间的转换关系:
| 范式 | 转换关系 |
|---|---|
| 1NF | 每一个分量是不可再分的数据项 |
| 2NF | 1NF消除了部分函数依赖后满足2NF |
| 3NF | 2NF消除了非主属性对码的传递函数依赖后满足3NF |
| BCNF | 3NF消除了主属性对码的部分和传递函数依赖后满足BCNF |
| 4NF | BCNF消除非平凡且非函数依赖的多值依赖后满足4NF |
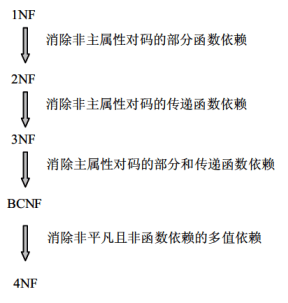
几种范式及其分解的性质:
| 性质 | 3NF | BCNF | 4NF |
|---|---|---|---|
| 消除函数依赖带来冗余 | 否 | 是 | 是 |
| 消除多值函数依赖带来冗余 | 否 | 否 | 是 |
| 保持函数依赖 | 是 | 否 | 否 |
| 保持多值函数依赖 | 否 | 否 | 否 |
数据库设计
新奥尔良(New Orleans)法式目前公认的数据库设计方法,它将数据库设计分为以下几个阶段:
- 用户需求分析
- 概念结构设计
- 逻辑结构设计
- 物理结构设计
这几个阶段之后是与数据库建立和运行有关的阶段:
- 数据库实施
- 数据库运行和维护
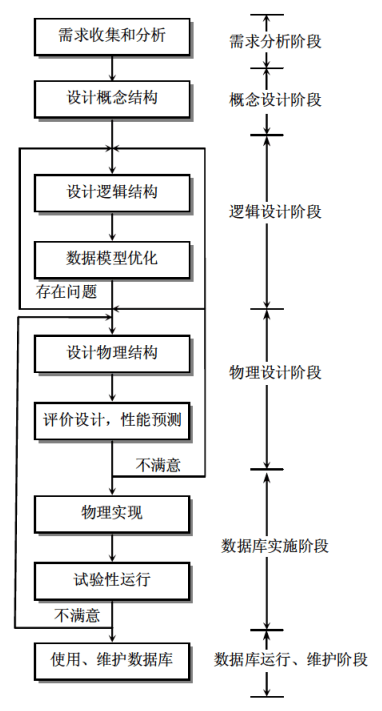
需求分析
需求分析是项目确定后,对数据库应用系统所要设计的内容(数据)和功能(行为)的整理和描述,是以用户的角度来认识系统。
需求分析是后面几个阶段,逻辑结构设计、物理结构设计以及应用程序设计的依据。
需求分析将收集到的零碎的、局部的数据分析整理后,建立需求说明文档、数据字典和数据流程图。
需求分析还包含:
-
数据流分析:是对事务处理所需的原始数据的收集,及经过处理后所得数据及其流向。
使用数据流图(DFD)表示。DFD能指出数据的流向和需要进行的事物处理(不涉及如何处理)。
-
数据字典:是关于数据库中数据的描述,即元数据(不是数据本身)。
数据字典包括5个部分:
- 数据项;
- 数据结构;
- 数据流;
- 数据存储;
- 加工。
系统需求说明书是需求分析阶段的成果,主要包括数据流图、数据字典、各种说明性表格、统计输出表和系统功能结构图等。
需求分析阶段的工作:
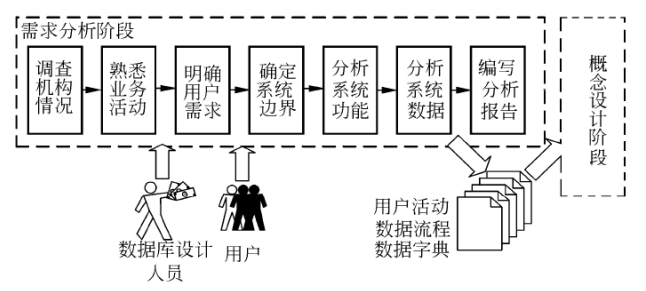
概念结构设计
概念设计阶段的目标是产生整体数据库概念结构,即概念模型,它是与DBMS无关的。
概念结构设计的方法:
- 自顶向下
- 自底向上
- 逐步扩张
- 混合策略(自顶向下和自底向上相结合)
概念结构是对现实世界的一种抽象,从数据库设计角度看,主要是数据抽象,一般有如下3种数据抽象:
- 分类
- 聚集
- 概括
局部视图设计就是对某个局部应用设计其分一R图,也称局部E-R图。其基本步骤如下:
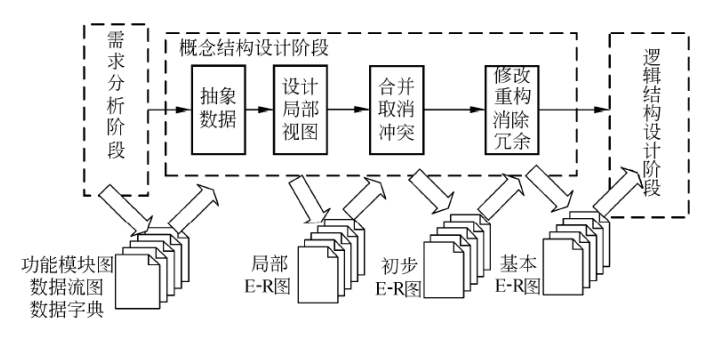
- 确定局部结构范围;
- 定义实体;
- 联系定义;
- 属性分配。
概念模型的建立采用E-R模型。
E-R 模型
E-R模型用E-R图(ERD)表示,E-R图有以下几个成分:
-
实体:用矩形表示。
-
联系:用棱形表示,并用无向边分别与有关实体连接起来,同时在无向边标注联系的类型($1:1$,$1:n$ 或 $m:n$)。
-
属性:用椭圆形表示,并用无向边将其与相应的实体连接起来
E-R模型中的属性有以下分类:
-
简单属性和复合属性:
- 简单属性是原子的、不可再分的;
- 复合属性可以细分为更小的部分。
-
单值属性和多值属性:
- 单值属性是一个属性对应一个值;
- 多值属性是一个属性对应一组值。
-
NULL属性:实体在某个属性上没有值或属性值未知时,使用NULL值表示。
-
派生属性:派生属性可以从其他属性得来(通过运算等方式求出)。
-
扩充的E-R模型(用来表达更多具有特殊语义的成分)有以下成分:
-
弱实体:使用双线矩形框表示。将需要依赖其他实体存在的实体。
实体间的所有(Ownership,拥有)关系代表一个实体对另一些实体具有很强的依赖关系,即一个实体的存在必须以另一个实体为前提。
例如职工与家属的联系,家属总是属于某职工的(在关系模式中需要依赖职工而存在),所以家属是弱实体。
-
特殊化:将一个实体集按照某些特性区分为几个子实体。这种从普遍到特殊的过程即为特殊化。
子实体的图形表示如下:

子实体由称为子类,它会有一个超类,并且能继承超类的属性,超类的属性是实体集中所有子实体的相同属性。
E-R图中的主要构件(包含扩充的E-R模型成分):
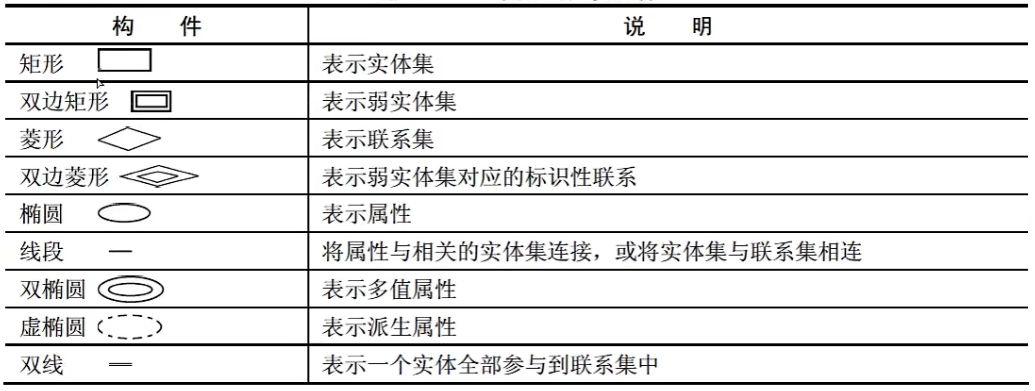
建立概念结构模型
建立概念结构模型的步骤如下:
-
选择局部应用:
需求分析阶段得到的大量数据分散杂乱,许多数据会应用于不同的处理,数据与数据之间关联关系也较为复杂。要最终确定实体、属性和联系,必须根据数据流图这一线索理清数据。
数据流图是对业务处理过程从高层到底层的一级抽象:
- 高层抽象流图一般反映系统的概貌,对数据的引用较为笼统;
- 底层又可能过于细致,不能体现数据的关联关系。
因此要选择适当层次的数据流图,让这一层的每一部分对应一个局部应用,实现某一项功能。从这一层入手,就能很好地设计分E-R图。
-
逐一设计分E-R图。
-
E-R图合并:
根据局部应用设计好各局部E-R图之后,就可以对各分E-R图进行合并。
合并的目的在于,在合并过程中解决分E-R图中相互存在的冲突。
分E-R图之间的冲突主要有:
- 属性冲突:同一属性在不同的分E-R图上的属性类型、取值范围和数据单位等可能会不一致。
- 命名冲突:相同意义的属性在不同的分E-R图上可能会有不同的命名。
- 结构冲突:同一实体在不同的分E-R图中可能会有不同的属性;同一对象在某一分E-R图中被抽象为实体,而在另一分E-R图中又可能被抽象为属性,反之亦然。
逻辑结构设计
逻辑结构设计就是在概念结构设计的基础上进行数据模型设计,可以是层次模型、网状模型和关系模型。
通常是把概念模型转换成为某个具体的数据库管理系统所支持的结构数据模型(与DBMS有关)。即,将概念结构设计所得的E-R模型转换成关系模式。
逻辑结构设计的工作步骤:
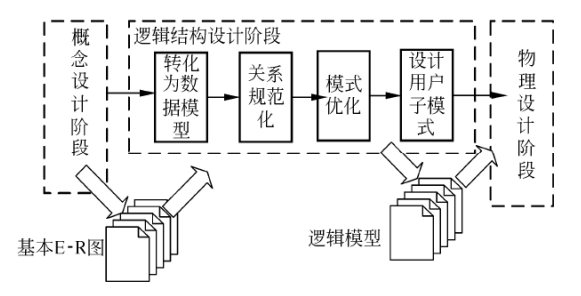
E-R 模型转换关系模式
-
实体向关系模式的转换:
将E-R图中的实体逐一转换成为一个关系模式:
- 实体名:对应关系模式的名称;
- 实体的属性:转换成关系模式的属性;
- 实体标识符:关系的码(键)。
超类和子类的转换:超类和子类定义为两个关系模式,将超类的主键加到子类中。
-
联系向关系模式的转换:
-
一对一联系的转换:
有两种方式:
-
方式1:将联系转换成一个独立的关系模式,关系模式的名称取联系的名称,关系模式的属性包括该联系所关联的两个实体的码及联系的属性,关系的码取自任一方实体的码。
那么一个一对一联系需要转换成三个关系模式。
-
方式2(一般使用该方式):将联系归并到关联的两个实体的任一方,给待归并的一方实体属性集中增加另一方实体的码和该联系的属性即可,归并后的实体码保持不变。
一个一对一联系仅需转换成两个关系模式。
例如:
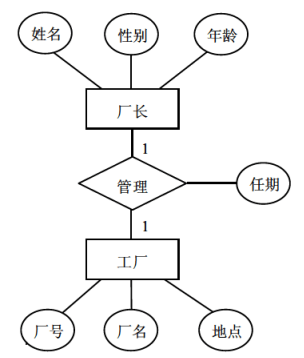
-
方式1:
厂长(姓名,性别,年龄)
工厂(厂号,厂名,地点)
管理((厂长)姓名,厂号,任期)
粗体代表该关系模式的码。管理的码可以为姓名或厂号。
-
方式2:
厂长(姓名,性别,年龄)
工厂(厂号,厂名,地点,(厂长)姓名,任期)
-
-
一对多联系的转换:
两种方式:
- 方式1:将联系转换成一个独立的关系模式,关系模式的名称取联系的名称,关系模式的属性取该联系所关联的两个实体的码及联系的属性,关系的码是多方实体的码;
- 方式2(一般使用该方式):将联系归并到关联的两个实体的多方,给待归并的多方实体属性集中增加一方实体的码和该联系的属性即可,归并后的多方实体码保持不变。
例如:
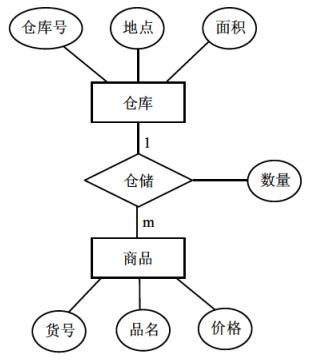
-
方式1:
仓库(仓库号,地点,面积)
商品(货号,商品名,价格)
仓储(货号,仓库号,数量)
-
方式2:
仓库(仓库号,地点,面积)
商品(货号,商品名,价格,仓库号,数量)
-
多对多联系的转换:
多对多联系只能转换成一个独立的关系模式,关系模式的名称取联系的名称,关系模式的属性取该联系所关联的两个多方实体的码及联系的属性,关系的码是多方实体的码构成的属性组。
例如:
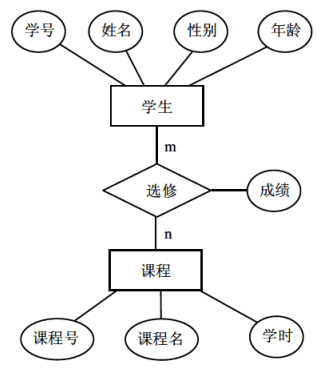
转换成:
学生(学号,姓名,性别,年龄)
课程(课程号,课程名,学时)
选修((学号,课程号),成绩)
-
关系模式的规范化
转换后的关系模式可能存在数据冗余、更新异常等问题,所以需要进一步的规范化处理。
-
根据语义确定各关系模式的数据依赖(函数依赖)。
-
根据数据依赖确定关系模式的范式。判定关系模式是否达到了3NF或4NF。
-
如果关系模式不符合要求,要根据关系模式的分解算法对其进行分解,达到3NF、BCNF或4NF。
-
关系模式的评价及修正。
根据规范化理论对关系模式分解之后,就可以在理论上消除冗余和更新异常。但根据处理要求,可能还需要增加部分冗余以满足处理要求,这就需要做部分关系模式的处理,分解、合并或增加冗余属性,提高存储效率和处理效率。
事务管理
事务是一个操作序列,这些操作“要么都做,要么都不做”。
事务和程序是两个不同的概念,一般一个程序可包含多个事务。
在SQL语言中,事务定义的语句有以下三条。
-
BEGIN TRANSACTION:事务开始。 -
COMMIT:事务提交。该操作表示事务成功地结束,它将通知事务管理器该事务的所有更新操作现在可以被提交或永久地保留。
-
ROLLBACK:事务回滚。该操作表示事务非成功地结束,它将通知事务管理器出故障了,数据库可能处于不一致状态,该事务的所有更新操作必须回滚或撤销。
事务的ACID性质:
-
原子性(Atomicity):事务是原子的,要么都做,要么都不做。
-
一致性(Consistency):事务执行的结果必须保证数据库从一个一致性状态变到另一个一致性状态。
因此,当数据库只包含成功事务提交的结果时,称数据库处于一致性状态。
-
隔离性(Isolation):事务相互隔离。
当多个事务并发执行时,任一事务的更新操作直到其成功提交的整个过程,对其他事务都是不可见的
-
持久性(Durability):一旦事务成功提交,即使数据库崩溃,其对数据库的更新操作也将永久有效。
数据库故障
在数据库的运行过程中,难免会出现计算机系统的软、硬件故障,这些故障会影响数据库中数据的正确性,甚至破坏数据库,使数据库中的全部或部分数据丢失。因此,数据库的关键技术在于建立冗余数据,即备份数据。如何在系统出现故障后能够及时地使数据库恢复到故障前的正确状态,就是数据库恢复技术。
故障类型:
- 事务内部故障:有的可以通过事务程序本身发现;有的是非预期的,不能由事务程序处理。
- 系统故障(软故障):是指造成系统停止运行的任何事件,使得系统要重新启动,例如CPU故障、操作系统故障和突然停电等。
- 介质故障(硬故障):如磁盘损坏、磁头碰撞和瞬时强磁干扰。此类故障发生的几率小,但破坏性最大。
- 计算机病毒:计算机病毒是一种人为的故障和破坏,是在计算机程序中插入的破坏,计算机功能或者数据可以繁殖和传播的一组计算机指令或程序代码。
备份方法
恢复的基本原理是“建立数据冗余”(重复存储)。建立冗余数据的方法是进行数据转储和登记日志文件,分为:
-
静态转储和动态转储:
-
静态转储:在转储期间不允许对数据库进行任何存取、修改操作;
-
动态转储:在转储期间允许对数据库进行存取、修改操作。
动态转储和用户事务可并发执行。
-
-
海量转储和增量转储:
- 海量转储:指每次转储全部数据;
- 增量转储:指每次只转储上次转储后更新过的数据。
-
日志文件:
在事务处理的过程中,DBMS把以下操作写入日志文件:
- 事务开始、事务结束;
- 对数据库的插入、删除和修改。
一旦发生故障,DBMS的恢复子系统利用日志文件撤销事务对数据库的改变,回退到事务的初始状态。因此,DBMS利用日志文件来进行事务故障恢复和系统故障恢复,并可协助后备副本进行介质故障恢复。
恢复
事务恢复有以下3个步骤:
- 反向扫描文件日志(即从最后向前扫描日志文件),查找该事务的更新操作。
- 对事务的更新操作执行逆操作。
- 继续反向扫描日志文件,查找该事务的其他更新操作,并做同样的处理,直到事务的开始标志。
并发控制
所谓并发操作,是指在多用户共享的系统中许多用户可能同时对同一数据进行操作。并发操作带来的问题是数据的不一致性,主要有三类:
- 丢失更新
- 不可重复读
- 读脏数据
其主要原因是事务的并发操作破坏了事务的隔离性。DBMS的并发控制子系统负责协调并发事务的执行,保证数据库的完整性不受破坏,避免用户得到不正确的数据。
封锁
并发控制的主要技术是封锁。基本封锁的类型有:
-
排它锁(X锁或写锁):若事务T对数据对象A加上X锁,则只允许T读取和修改A,其他事务都不能再对A加任何类型的锁,直到T释放A上的锁。
-
共享锁(S锁或读锁):若事务T对数据对象A加上S锁,则只允许T读取A,但不能修改A,其他事务只能再对A加S锁,直到T释放A上的S锁。
这就保证了其他事务可以读A,但在T释放A上的S锁之前不能对A进行任何修改。
分布式数据库
分布式数据库系统是指数据存放在计算机网络的不同场地的计算机中,每一场地都有自治处理能力并能完成局部应用;而每一场地也参与(至少一种)全局应用程序的执行,全局应用程序可通过网络通信访问系统中多个场地的数据。其定义强调分布性和逻辑整体性两点。
分布式数据库中有以下基本概念:
- 分片透明:指用户或应用程序不需要知道逻辑上访问的表具体是怎么分块存储的。
- 复制透明:指采用复制技术的分布方法,用户不需要知道数据是复制到哪些节点,如何复制的。
- 位置透明:指用户无须知道数据存放的物理位置。
- 逻辑透明:指用户或应用程序无需知道局部场地使用的是哪种数据模型。
具有以下性质:
- 共享性:数据存储在不同的结点数据共享。
- 自治性:指每结点对本地数据都能独立管理。
- 可用性:指当某一场地故障时,系统可以使用其他场地上的副本而不至于使整个系统瘫痪。
- 分布性:指数据在不同场地上的存储。
存储过程
存储过程(Stored Procedure)是在大型数据库系统中,一组为了完成特定功能的SQL语句集,它存储在数据库中,一次编译后永久有效,用户通过指定存储过程的名字并给出参数(如果该存储过程带有参数)来执行它。
存储过程是数据库所提供的一种数据库对象,通过存储过程定义一段代码,提供给应用程序调用来执行。从安全性的角度考虑,更新数据时,通过提供存储过程正第三方调用,将需要更新的数据传入存储过程,而在存储过程内部用代码分别对需要的多个表进行更新,从而避免了向第三方提供系统的表结构,保证了系统的数据安全。


评论