复杂度

算法时间复杂度以算法中基本操附重复执行的次数（简称为频度）作为算法的时间度量。一般不必要精确计算出算法的时间复杂度，只要大致计算出相应的数量级即可，使用大$O$表示法表示（空间复杂度也是）。

• 加法规则：多项相加，保留最高阶项，并将系数化为1；
• 乘法规则：多项相乘都保留，并将系数化为1。

递归式的时间（空间）复杂度：

$$ 递归的次数 \times 每次递归的时间（空间）复杂度 $$

逻辑结构分类

• 线性结构
  • 线性表（一般线性表）
  • 特殊线性表
    • 栈
    • 队列
    • 字符串
  • 线性表的推广
    • 数组
    • 广义表
• 非线性结构
  • 树结构
    • 二叉树
    • 多叉树
  • 图结构
    • 有向图
    • 无向图
  • 集合结构

---

线性表

由 $n(n \geq 0)$ 个数据特性相同的元素构成的有限序列称为线性表。$n=0$ 时，称为空表。非空表的特点如下：

• 存在唯一一个“第一个”元素。
• 存在唯一一个“最后一个”元素。
• 相邻元素之间存在序偶关系：
  • 除第一个之外，结构中的每个数据元素均只有一个前驱；
  • 除最后一个之外，结构中的每个数据元素均只有一个后继。

线性表的存储结构分为：

• 顺序存储；
• 链式存储

顺序存储结构

线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻。在这种存储方式下，元素间的逻辑关系无须占用额外的空间来存储。

其存储结构如图所示：

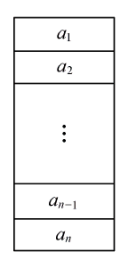
假设线性表的每个元素占用的存储空间为$L$，$LOC(a_i)$为第$i$个元素的存储位置（$0 \le i \le n-1$，$n$为线性表的长度）：

• 第$i+1$个元素和第$i$个元素的存储位置满足：

  $$ LOC(a_{i+1})=LOC(a_i)+L $$

• 第$i$个元素的存储位置：

  $$ LOC(a_i)=LOC(a_0) + i \times L $$

  如果下标从1开始：

  $$ LOC(a_i)=LOC(a_1) + (i-1) \times L $$

顺序存储结构的线性表的特点：

• 优点：可以随机存取表中的元素，不需要额外的存储空间来表达元素之间的逻辑关系；
• 缺点：插入和删除操作不方便、效率低、比较耗时（插入和删除操作需要移动元素），顺序表的长度是固定的。

在表为$n$的线性表中，有$n+1$个插入位置（不考虑插入是否会导致溢出）：

• 在第$i$个插入位置插入，需要移动$n+1-i$个元素。

  • 在第1个位置插入（$a_1$）需要移动$n$个元素；
  • 在第$n+1$个位置插入（$a_n$后面）不需要移动元素。

• 设在第$i$个插入位置插入的概率为$p_i$，等概率下（假如这$n+1$个插入位置插入的概率相同）插入一个新元素需要移动的元素个数的期望值$E_{insert}$为：

  $$ E_{insert} = \sum_{i=1}^{n+1}{ \Big( p_i \times (n-i+1) \Big) } = \cfrac{1}{n+1} \sum_{i=1}^{n+1}{(n-i+1)} = \cfrac{n+1}{2} $$

  $$ p_i = \cfrac{1}{n+1} $$

  即，$E_{insert} = \cfrac{插入位置数-1}{2} = \cfrac{n+1}{2}$

在表长为$n$的线性表中删除元素时，共有$n$个可删除的元素：

• 删除第$i$个元素$a_i$需要移动$n-i$个元素。

  • 删除元素$a_1$需要移动$n-1$个元素；
  • 删除元素$a_n$不需要移动元素。

• 设$a_i$被删除的概率为$q_i$，等概率下删除元素时需要移动的元素个数的期望值$E_{delete}$为：

  $$ E_{delete} = \sum_{i=1}^{n}{\Big( q_i \times (n-i) \Big)} = \cfrac{1}{n} \sum_{i=1}^{n}{(n-i)} = \cfrac{n-1}{2} $$

  $$ q_i = \cfrac{1}{n} $$

  即，$E_{delete} = \cfrac{删除位置数}{2} = \cfrac{n-1}{2}$

插入操作时间复杂度：

• 最好情况（在第$n+1$个位置插入）：$O(1)$；
• 最坏情况（在第1个位置插入）：$O(n)$；
• 平均复杂度：$O(n)$。

查找元素时间复杂度（根据下标查找）：$O(1)$。

累加求和公式：

$$ \sum_{i=0}^{n} i = \cfrac{n(1+n)}{2} $$

即等差数列求和中的：

$$ S_n = \cfrac{n(a_1 + a_n)}{2} $$

链式存储结构

线性表的链式存储是指通过指针链接起来的结点来存储数据元素。

其存储结构如下所示：

• 数据域：用于存储数据元素的值；

• 指针域：用于存储当前元素的直接前驱或直接后继的位置信息（直接前或后驱的指针，称其为指针或链）。

  存储各数据元素的结点的地址并不要求是连续的，因此存储数据元素的同时必须存储元素之间的逻辑关系。

链式表的特点：

• 结点空间只有在需要的时候才申请，无须事先分配；
• 长度不固定。

链式表结点之间通过指针域构成一个链表，若结点中只有一个指针域，则称为线性链表。

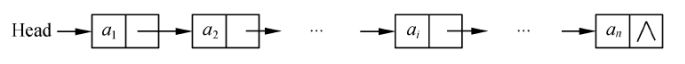
上图中的Head：一个指向链表第一个结点的针，称为头指针。使用它就可以顺序地访问到表中的任意一个元素。

插入和删除操作时间复杂度（带不带头节点的复杂度都一样）：

• 最好情况（在$i=1$位置）：$O(1)$；
• 最坏情况（在$n+1$位置插入/删除$n$位置）：$O(n)$
• 平均复杂度：$O(n)$

链表操作的时间复杂度取决于指针遍历。

---

栈

栈是一种后入先出（Last In First Out，LIFO）的线性表。栈只能通过访问它的一端来实现数据存储和检索。

栈的基本操作有：

• 入栈：将元素置入栈顶；
• 出栈：将元素从栈顶中取出。
• 读取栈顶元素

栈的出栈顺序一定和入栈顺序相反。

顺序存储结构

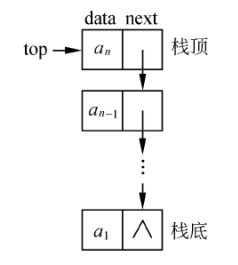
栈的顺序存储结构也称为顺序栈。

顺序栈使用一个栈顶指针标记栈顶元素的索引位置。每次出栈时都需要重置栈顶指针，将栈顶指针向下移动，标记到新的栈顶元素。

顺序栈的空间容量有限，所以每次入栈时都需要判断栈是否为满。

链式存储结构

栈的链式存储结构称为链栈。链栈的头指针就是栈顶指针。

栈的应用

栈的典型应用包括表达式求值、括号匹配等，在计算机语言的实现以及将递归过程转变为非递归过程的处理中，栈有重要的作用。

---

队列

队列是一种先入先出（First In First Out，FIFO）的线性表。

队列只允许在表的一端插入元素，在表的另一端删除元素。

• 队头（Front）：允许删除元素的一端；
• 队尾（Rear）：允许插入元素的一端。

队列的基本操作有：

• 入队：将元素加入到队尾；
• 出队：将元素加入到对头。

队列的入队顺序一定等于出队顺序。

使用两个栈可以来模拟一个队列（从一个栈出栈后的元素入另一个栈后再出栈）。

顺序存储结构

队列的顺序存储结构称为顺序队列。

顺序队列设置两个指针：

• 队头指针：指向对头元素的下标；
• 队尾指针：指向队尾元素的下标。

如果顺序队列只按照数组下标大小顺序来设置指针（对头指针的值永不大于队尾指针），那么在经过一段时间的操作后，对头指针有可能指向的并不是数组的第一个元素，此时队列的长度永远都到达不了数组的长度（空间无法被充分利用，实际使用的长度和逻辑长度不符）。

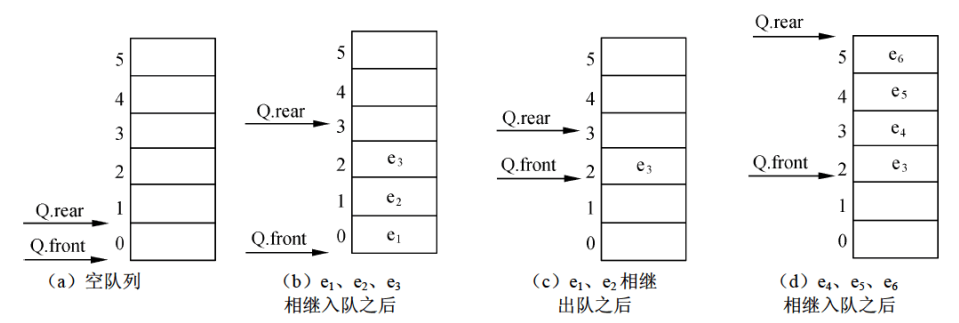
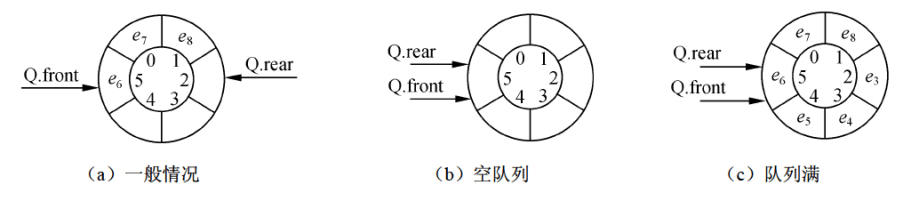
为了解决这个问题，我们可以把数组想象为一个环型的结构（将最后一个元素和第一个元素连接起来，队头指针可以比队尾指针大）。如果此时队列的状态是上图中步骤$(e)$的状态，此时再插入元素，可以将元素放在数组索引0的位置，再让队尾指针始终保持在队列最后一个元素的索引之后即可。将这种队列称为循环队列，如：

链式存储结构

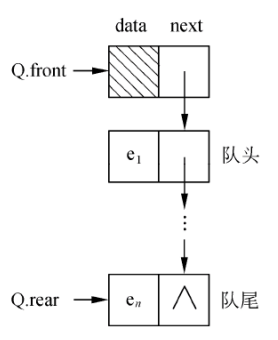
队列的链式存储也称为链队列（链队）。这里为了便于操作，可以给链队列添加一个头结点，并令头指针指向头结点。因此，队列为空的判定条件是头指针和尾指针的值相同，且 均指向头结点。

队列的应用

队列结构常用于处理需要排队的场合，例如操作系统中处理打印任务的打印队列、离散事件的计算机模拟等。

---

串

串（字符串）是一种特殊的线性表，其数据元素为字符。

串具有自身的特性，运算时常常把一个串作为一个整体来处理。

串的基本概念和操作：

• 空串：长度为0的串；

• 子串：由串中任意长度的连续字符构成的序列称为子串。含有子串的串称为主串。子串在主串中的位置是指子串首次出现时，该子串的第一个字符在主串中的位置。空串是任意串的子串。

• 串相等：指两个串长度相等且对应序号的字符也相同。

• 串比较：两个串比较大小时以字符的ASCⅡ码值（或其他字符编码集合）作为依据。

  实质上，比较操作从两个串的第一个字符开始进行，字符的码值大者所在的串为大；若其中一个串先结束，则以串长较大者为大。

• 赋值：

  • 拷贝赋值：将一个串的值赋给另一个串；
  • 引用（地址）赋值：将一个串的引用（地址）赋给另一个串。那么这个串可以使用另一个串中的值，但是对这个串所做的操作，也会作用到另一个串。

• 连接串：将一个串插入到另一个串尾。

• 插入串：将一个串插入到另一个串的任意位置中。

顺序存储结构

串的顺序存储结构是一种定长的串（类似顺序表）。

链式存储结构

串的链式存储结构可以方便地对串进行插入删除操作（类似链表）。

串的模式匹配

子串的定位操作通常称为串的模式匹配。子串也称为模式串。

有关串模式匹配算法的详细讲解可以查看：经典字符串匹配

朴素的模式匹配算法

朴素的模式匹配算法也称为布鲁特一福斯算法（即暴力匹配算法），其基本思想是从主串的第一个字符起与模式串的第一个字符比较，若相等，则继续逐一对字符进行后续的比较，否则从主串第二个字符起与模式串的第一个字符重新比较，直到模式串中每个字符依次和主串中一个连续的字符序列相等时为止，此时称为匹配成功。如果不能在主串中找到与模式串相同的子串，则匹配失败。

设主串和模式串的长度分别为$n$和$m$，算法时间复杂度和比较次数：

• 最好情况：$O(m)$，次数为$m$；

• 最坏情况：$O(n \times m)$，次数为$\cfrac{1}{2} m(n-m+2)$：

  $$ \sum_{i=0}^{n-m}{p_i\big( (i+1) \times m \big)} = \cfrac{m}{n-m+1} \sum_{i=0}^{n-m}{(i+1)} = \cfrac{1}{2} m(n-m+2) $$

• 平均：$O(n+m)$，次数为$\cfrac{1}{2} (n+m)$：

  $$ \sum_{i=0}^{n-m}{p_i(i+m)} = \cfrac{1}{n-m+1} \sum_{i=0}^{n-m}{i+m} = \cfrac{1}{2} (n+m) $$

KMP 算法

KMP算法又称为改进的模式匹配算法。

• 串的前缀：包含第一个字符，且不包含最后一个字符的子串；
• 串的后缀：包含最后一个字符，且不包含第一个字符的子串。
• 前缀集合：包含串的所有前缀的集合；
• 后缀集合：包含串的所有后缀的集合。

KMP的重点是求模式串字符的next值（失配指针$Next[\ i\ ]$），假设$a_{i-1}$为当前要求next值的模式串字符：

• 前缀集合：

  $$ Prefix=\{p_0,p_0p_1,\cdots,p_0…p_{i-1}\} $$

• 后缀集合：

  $$ Postfix=\{p_{i-1},p_{i-2}p_{i-1},\cdots,p_1…p_{i-1}\} $$

• 失配指针：

  $$ Next[i] = \begin{cases} -1 & 当\ i=0 时 \\ max & \{ k|0<k<i 且 “p_0\cdots p_{k-1}” = “p_{i-k}\cdots p_{i-1}” \} \\ 0 & 其他情况 \end{cases} $$

  即：

  • $Next[0] = -1$；
  • $Next[i] = maxLen(Prefix \cap Postfix)$

  可以解释为：

  $$ Next[\ i\ ] = 前i个子串的最长相同前后缀的长度 $$

  特殊情况：$Next[\ 1\ ] = 0$，因为其前缀集合和后缀集合都为空。

失配表是用来指示匹配失败后指针该如何移动的。

失配表的建立跟要匹配的串没有任何关系，仅跟模式串有关。

---

多维数组

多维数组是定长线性表在维数上的扩展，即线性表中的元素又是一个线性表。多维数组是一种“同构”的数据结构，其每个数据元素类型相同、结构一致。

• 一维数组：即线性表。

• 二维数组（仅讨论顺序存储结构）：

  二维数组的存储结构（如下图），可以分为以行为主序（下图左边）和以列为主序（下图右边）两种。

  

  设：

  • 二维数组为$A[n,m]$，$n$为行数，$m$为列数；
  • 数组元素$a_{i,j},\ 0 \le i \le n-1,\ 0 \le j \le m-1$；
  • $LOC(a_{i,j})$为元素$a_{i,j}$的地址；
  • $L$为单个元素的存储空间大小。

  则有：

  • 以行为主序优先存储：

    $$ LOC(a_{i,j}) = LOC(a_{0,0}) + (i \times n + j) \times L $$

    如果下标从1开始（$1 \le i \le n,\ 1 \le j \le m$）：

    $$ LOC(a_{i,j}) = LOC(a_{1,1}) + \big( (i-1) \times n + (j-1) \big) \times L $$

  • 以列为主序优先存储：

    $$ LOC(a_{i,j}) = LOC(a_{0,0}) + (i + j \times m) \times L $$

    如果下标从1开始（$1 \le i \le n,\ 1 \le j \le m$）：

    $$ LOC(a_{i,j}) = LOC(a_{1,1}) + \big( (i-1) + (j-1) \times m \big) \times L $$

优先存储说法问题：

以行为主序优先存储的意思应该是在内存中按行存储。以列为主序优先存储的意思应该是在内存中按列存储。

假设一个二维数组为：

$$ \begin{vmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ a_{51} & a_{52} & a_{53} & a_{54} \end{vmatrix} $$

按照以行为主序优先存储的公式，它在内存中应该是分为了5个地址连续的数组来存储。即内存中，$[a_{11},a_{12},a_{13},a_{14}]$为一个数组，其后再接一个数组$[a_{12},a_{22},a_{23},a_{24}]$，以此类推，在内存中按照列的元素作为一个连续的一维数组单位，再按照第1行后接第2行作为整个连续的二维数组。它们在内存中的地址顺序是：

$$ a_{11},a_{12},…,a_{14},\\ a_{21},…,a_{24},\\ a_{31},…,a_{34},\\ a_{41},…,a_{44},\\ a_{51},…,a_{54} $$

那么以列为主序优先存储的地址顺序就为：

$$ a_{11},a_{21},…,a_{51},\\ a_{12},…,a_{52},\\ a_{13},…,a_{53},\\ a_{14},…,a_{54} $$

一般矩阵都用二维数组来表示，但是对于一些特殊矩阵，如对称矩阵、三角矩阵和对角矩阵。它们的非0元素的分布存在一定规律，所以可以将其压缩存储在一维数组中，并且它们的多个值相同的元素（按照对应特殊矩阵定义上的值相同，并非简单的值相同）只分配一个存储单位。

对称矩阵

若矩阵$A_{n \times n}$中的元素特点为$a_{ij}=a_{ji}\ (1 \le i,j \le n)$，则称之为$n$阶对称矩阵。

对称矩阵$A_{n \times n}$：

$$ \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} $$

其中以对角线划分为三个区域：

• 主对角线：$a{11},a_{22},\cdots,a_{nn}$，共有$n$个元素；

• 上三角区：对角线以上的所有元素，即：

  $$ \begin{vmatrix} 0 & a_{12} & a_{13} & \cdots & a_{1n} \\ 0 & 0 & a_{23} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{(n-1)n} \\ 0 & 0 & 0 & \cdots & 0 \end{vmatrix} $$

• 下三角区：对角线以下的所有元素，和上三角区的个数相等并且重复。

可以将对称矩阵中，$n^2$个元素压缩存储到$\cfrac{n(n+1)}{2}$个元素的存储空间中。一般是存储下三角区和对角线。

假设将$n$阶对称矩阵$A_{n \times n}$压缩存储到一维数组$B\left[ \cfrac{n(n+1)}{2} \right]$，则$B[k]\ (1 \le k \le \cfrac{n(n+1)}{2})$与矩阵元素$a_{ij}(a_{ji})\ (1 \le i,j \le n)$之间存在一一对应关系（以行为主序）：

$$ k = \begin{cases} \cfrac{i(i-1)}{2} + j, & 当\ i \ge j \\ \cfrac{j(j-1)}{2} + i, & 当\ i < j \end{cases} $$

如果下标从0开始（第一个元素为$a_{00}$，$0 \le k \le \cfrac{n(n+1)}{2} - 1$，并且$0 \le i,j \le n-1$）：

$$ k = \begin{cases} \cfrac{i(i+1)}{2} + j + 1, & 当\ i \ge j \\ \cfrac{j(j+1)}{2} + i + 1, & 当\ i < j \end{cases} $$

为什么$length(B) = \cfrac{n(n+1)}{2}$（压缩存储的一维数组大小）：

主对角线的元素的大小为$n$，下三角区的对角线大小分别为$n-1,n-2,…,1$。即： $$ length(B) = \sum_{i=1}^{n}{i} = \cfrac{n(n+1)}{2} $$

PS：《软件设计师教程（第五版）》中一维数组的下标$k$的取值范围错了：

很明显不是$\left[ 1, \cfrac{n(n+1)}{2} \right)$，而应该是$\left[ 1, \cfrac{n(n+1)}{2} \right]$。

三对角矩阵

对角矩阵是指矩阵中的非0元素都集中在以主对角线为中心的带状区域中，即除了主对角线上和直接在对角线上、下方若干条对角线上的元素外，其余的矩阵元素都为0。三对角矩阵是对角矩阵中的一种，包括主对角线和在主对角线上、下方的各一条对角为非0元素：

$$ \begin{vmatrix} a_{11} & a_{12} & 0 & \cdots & 0 & 0 \\ a_{21} & a_{22} & a_{23} & \cdots & 0 & 0 \\ 0 & a_{32} & a_{33} & \cdots & 0 & 0 \\ 0 & 0 & a_{43} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & a_{(n-1)(n-1)} & a_{(n-1)n} \\ 0 & 0 & 0 & \cdots & a_{n(n-1)} & a_{nn} \end{vmatrix} $$

设有$n$阶三对角矩阵$A_{n \times n}$，将其非0元素$a_{ij}(a_{ji})\ (1 \le i,j \le n)$存储在一维数组$B[k](1 \le k \le 3 \times n - 2)$中，则元素位置之间的对应关系为：

$$ k = 3 \times (i-1) - 1 + j - i + 1 + 1 = 2i + j -2 $$

如果下标从0开始（$0 \le k \le 3(n-1)$，并且$0 \le i,j \le n-1$）：

$$ k = 3 \times i - 1 + j - i + 1 + 1 = 2i + j + 1 $$

稀疏矩阵

在一个矩阵中，若非0元素的个数远远少于0元素的个数，且非0元素的分布没有规律，则称之为稀疏矩阵。

对于稀疏矩阵，存储非0元素时必须同时存储其位置（即行号和列号），用三元组$(i,j,a_{ij})$可唯一确定矩阵$A$中的一个元素。

可以用三元组表来存储这些三元组。稀疏矩阵的三元组表的顺序存储结构称为三元组顺序表，常用的三元组表的链式存储结构是十字链表。

---

树

树结构是一种非线性结构，该结构中的一个数据元素可以有两个或两个以上的直接后继元素。

树（Tree）是 $n(n\ge0)$ 个结点的有限集。

• 空树：$n=0$；
• 非空树：$n>0$，
  • 有且仅有一个根结点，
  • 除根节点外的其余结点可分为 $m(m>0)$ 个互不相交的集合，即子树（SubTree）$T_1,T_2,\cdots,T_m$。

树的定义是递归的：

• 一棵树由若干棵子树构成；
• 子树又由更小的子树构成。

基本概念

术语

• 度：结点拥有的子树数。整个树的度是树内各结点度的最大值。
• 叶结点：度为 0 的结点，也称终端结点。
• 非终端结点：度不为 0 的结点，也称分支结点。
• 内部结点：除根节点外的非终端结点。
• 子节点：结点子树的根结点。
• 父结点：与子结点相连的上一层的唯一一个结点。
• 兄弟结点：同一个父节点的子节点之间互为兄弟。
• 祖先结点：从根结点到该结点所经分支上的所有结点（包括其父节点，但不包括其本身）。
• 子孙结点：以某结点为根的子树中的所有结点。
• 堂兄弟结点：父节点在同一层（但不是同一个）的结点互为堂兄弟。
• 层次：以根结点为第一层，根的子节点为第二层 …… 树中任意结点的层次等于其父节点的层次加 1。
• 树的高度：树中结点的最大层次，也称树的深度。
• 森林：是 $m(m\ge0)$ 棵互不相交的树的集合。树中每个结点的子树的集合即为森林。

树的类型

• 有序树：树中结点的各子树从左到右是有次序的，即不能互换。
• 无序树：树中结点的各子树相互之间可以互换，没有次序。

树的性质

• 设$n$个结点的树，$d_i \ (1 \le i \le n)$为该树中结点的度：

  $$ n = (\sum_{i=1}^{n}{d_i})+1 $$

• 度为$m$的树中第$i$层上至多有$m^{i-1}$个结点（$i \ge 1$）。

• 高度为$h$的$m$度树至多有$\cfrac{m^h-1}{m-1}$个结点。

树的逻辑结构

树可以用二元组 $Tree=(root,F)$ 表示。其中 $root$ 是根结点，$F$ 是 $m(m\ge0)$ 棵子树的森林，即 $F=(T_1,T_2,\cdots,T_m)$，其中 $T_i=(r_i,F_i)$ 为根 $root$ 的第 $i$ 棵子树。

树根与其子树森林之间的关系： $$ RF = \{ <root,r_i>|i=1,2,4,m,\quad m>0 \} $$

---

二叉树

二叉树是（$n \ge 0$）个结点的有限集合：

• 空树：$n=0$；
• 由一个根结点及两棵不相交的且分别称为左、右子树的二叉树所组成（两个子数顺序不可交换）。

二叉树同样具有递归性质。

二叉树的性质：

• 第$i$层（$i \ge 1$）上最多有$2^{i-1}$个结点。

  因为二叉树每个结点至多有两个分支（结点）。

• 高度为$k$的二叉树最多有$2^k-1$个结点（$k \ge 1$）。

  每层结点都取最大值后累加：

  $$ \sum_{i=1}^{k}{2^{i-1}} = 2^k - 1 $$

  将深度为$k$且有$2^k-1$个结点的二叉树称为满二叉树。

  对满二叉树自上而下、从左至右进行编号（即层序遍历的顺序）。一个深度为$k$、有$n$个结点的二叉树，当且仅当其每一个结点都于深度为$k$的满二叉树中编号从1至$n$的结点一一对应时，称之为完全二叉树。

  完全二叉树有一个隐藏关系：$n > 2^{k-1}-1$。即深度为$k$的完全二叉树，其结点数$n$必须要比深度为$k-1$的满二叉树至少多1个结点。

  深度为$k$的满二叉树结点数$n$和其第$k$层结点数$m$的关系：

  $$ n = 2m-1 $$

• 任何一棵二叉树，若其终端结点数（度为0的结点数）为$n_0$，度2的结点数为$n_2$，则$n_0=n_2+1$。

  即：

  $$ 终端结点数（度0结点数）=度2结点数+1 $$

• 具有$n$个结点的完全二叉树的深度（高度）为：

  $$ \lfloor \log_2{n} \rfloor + 1; $$

  或：

  $$ \lceil \log_2{(n+1)} \rceil $$

二叉树形态总数（卡特兰数）：

$$ \cfrac{C^{n}_{2n}}{n+1} $$

排列组合公式：

$$ A^n_m = m \times (m-1) \times \cdots \times (m-n+1) $$

$m$是起点，$n$是次数。

$$ C^n_m = \cfrac{A^n_m}{A^n_n} $$

顺序存储结构

用一组地址连续的存储单元存储二叉树中的结点。

可以按照为完全二叉树编号的顺序（即层序遍历的顺序），将二叉树映射到顺序表中：

若编号为$i$的结点（$i \ge 1$），则：

• $i=1$：根结点，没有双亲（父结点）；
• $i>1$：双亲为$\left\lfloor \cfrac{i}{2} \right\rfloor$；
• $i \le \cfrac{n}{2}$：左孩子编号为$2i$；
• $i \le \cfrac{n-1}{2}$：右孩子编号为$2i+1$。

完全二叉树适合采用顺序存储结构，而一般二叉树则不适合。

链式存储结构

可以用三叉链表或二叉链表来存储二叉树（一个结点含有3个或2个指针，其中必须有两个指针来分别存储左子树和右子树的根结点）。链表的头指针指向二叉树根结点：

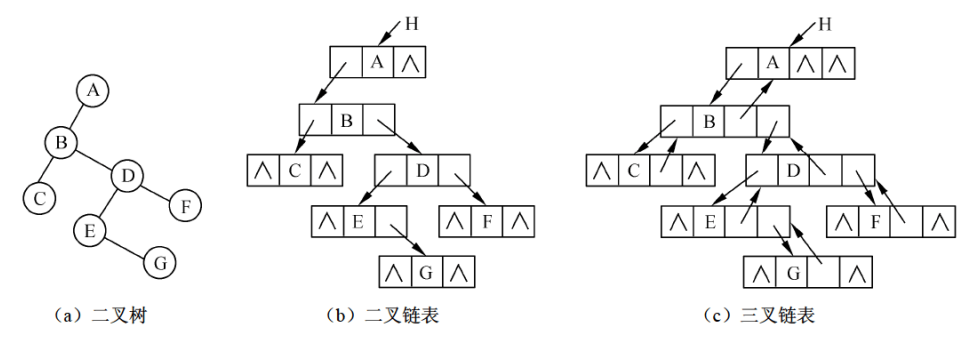
三叉链表仅仅是多了一个指向父结点的链表。

设有$n$个结点的二叉树，则其空指针域数量：

• 对于二叉链表：

  • 总指针域个数：$2n$；
  • 分支数（子孙结点数，非空指针域个数）：$n-1$。

  可得：

  $$ 空指针域数=2n-(n-1)=n+1 $$

• 对于三叉链表：

  • 总指针域个数：$3n$；
  • 分支数（子孙结点数）：$n-1$；
  • 指向父结点且非空的指针域个数：$n-1$。

  即，非空指针域个数为：$2(n-1)$。

  可得：

  $$ 空指针域数=3n-2(n-1)=n+2 $$

遍历

二叉树有以下遍历方法：

• 先序遍历：根左右

  1. 访问根结点；
  2. 先序遍历左子树；
  3. 先序遍历右子树。

• 中序遍历：左根右

  1. 中序遍历左子树；
  2. 访问根结点；
  3. 中序遍历右子树。

• 后序遍历：左右根

  1. 后序遍历左子树；
  2. 后序遍历右子树；
  3. 访问根结点。

  后序遍历可以使用栈：

  1. 根结点入栈；
  2. 右子树（如果有的话）按照步骤1至3顺序入栈（先入根结点，然后入右子树，再入左子树）；
  3. 左子树（如果有的话）按照步骤1至3顺序入栈（先入根结点，然后入右子树，再入左子树）；
  4. 将栈中所有元素出栈，出栈顺序即为后序遍历的顺序。

• 层序遍历：根据层序从上至下，从左到右遍历

  1. 访问根结点（第1层）；

  2. 从左到右访问第2层所有结点；

  3. 从左到右访问第3层所有结点；

     …

  直至访问到最后一层的所有结点（从左到右）。

  层序遍历可以使用队列：

  1. 将根结点入队；
  2. 将对头元素出队，然后将其左右子结点（如果有的话）依序入队；
  3. 重复步骤2直至所有元素出队，出队顺序即为层序遍历顺序。

二叉树的遍历实质上是对一个非线性结构进行线性化的过程，它使得每个结点（除第一个和最后一个）在这些线性序列中有且仅有一个直接前驱和直接后继。

平衡二叉树

二叉树可以用于快速查找。例如比根结点小的在左子树，比根结点大的在右子树（二叉排序树）。那么每次查找，根据根结点就可以剔除一半的范围。

但是如果二叉树左右子树的结点数量差别很大，那么每次查找并不一定能剔除一半的范围，查询效率大打折扣。

设一个二叉树的左右子树高度之差的绝对值为$d$，那么

• 不平衡的二叉树：$d > 1$；
• 平衡的二叉树：$d \le 1$。

完全二叉树一定是平衡二叉树，平衡二叉树不一定是完全二叉树。

二叉排序树

二叉排序树的定义：

• 左子树所有结点的关键字都小于根结点；
• 右子树所有根结点的关键字都大于根结点；
• 左右子树也都是二叉排序树。

二叉排序树的中序遍历（左根右）得到的是该二叉树的有序序列。

线索二叉树

线索二叉树是在二叉树结点中保存了结点的前驱和后继的信息。

如果使用指针来指向其前驱和后继，增加指针信息会降低存储空间的利用率。

可以采用增加两个标志（leftTag和rightTag）来区分指针域指向的是左或右子结点还是前驱或后继：

leftTag

leftChild

data

rightChild

rightTag

其中：

$$ leftTag = \begin{cases} True & leftChild指向结点左孩子 \\ False & leftChild指向结点的直接前驱 \end{cases} $$

$$ rightTag = \begin{cases} True & rightChild指向结点右孩子 \\ False & rightChild指向结点的直接后继 \end{cases} $$

若二叉树的二叉链表采用以上所示的结点结构，则相应的链表称为线索链表，其中指向结点前驱、后继的指针称为线索。

对二叉树以某种次序遍历使其成为线索二叉树的过程称为线索化。

哈夫曼树

哈夫曼树即最优二叉树，是一类带权路径长度最短的树。

• 路径：指从树中一个结点到另一个结点之间的通路；

• 路径长度：路径上的分支数目；

• 树的路径长度：指从树根到每一个叶子之间的路径长度之和；

• 结点的带权路径长度：从该结点到树根之间的路径长度与该结点权值的乘积；

• 树的带权路径长度：树中所有叶子结点的带权路径长度之和。

  设：

  • 带权叶子结点数：$n$；
  • 叶子结点的权值：$w_k$；
  • 叶子结点到根的路径长度：$l_k$。

  则树的带权路径长度为：

  $$ WPL = \sum_{k=1}^{n}{w_kl_k} $$

哈夫曼树是指权值为$w_1,w_2,\cdots,w_n$的$n$个叶子结点的二叉树中，带权路径长度最小的二叉树。

构造最优二叉树的哈夫曼算法：

1. 根据给定的$n$个权值$\{ w_1,w_2,\cdots,w_n \}$，构成$n$棵二叉树集合$F=\{T_1,T_2,\cdots,T_n\}$，每棵树$T_i$有且仅有一个带权为$w_i$的根结点。
2. 在$F$中选取2棵权值最小的树作为左、右子树，构造一棵新二叉树。新二叉树的根结点权值为其左右子树根结点权值之和。
3. 从$F$中删除这2棵树，并将新树加入到$F$中。
4. 重复步骤2、3直到$F$中仅含一棵树为止，这棵树便是哈夫曼树。

哈夫曼算法并未规定哪棵树作为左或右子树，所以哈夫曼树并不唯一，但$WPL$值是唯一的。

给定$n$个权值后，哈夫曼树的结点数$m$就确定了：

$$ m = 2 \times n - 1 $$

所以可用一维数组存储哈夫曼树。

哈夫曼编码

哈夫曼编码是一种不等长的编码，它用哈夫曼算法来构造出最优前缀码：

给定字符集$D=\{ d_1,d_2,\cdots,d_n \}$及字符的使用频率$W=\{w_1,w_2,\cdots,w_n\}$。

构造最优前缀码的方法为：

1. 以$d_1,d_2,\cdots,d_n$作为叶子结点，$w_1,w_2,\cdots,w_n$作为叶子结点的权值，构造出一棵最优二叉树。
2. 将树中每个结点的左分支标上0，右分支标上1（左0右1）。
3. 每个叶子结点代表字符的编码就是从根到叶子的路径上组成的0、1串。

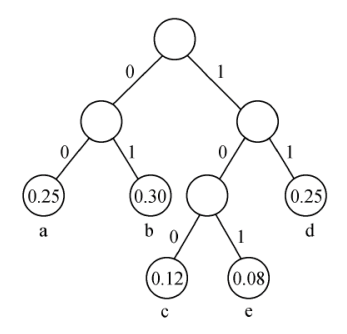
其中，字符$a$字符$b$、$c$、$d$、$e$的编码分别为00、01、100、11、101。

压缩比

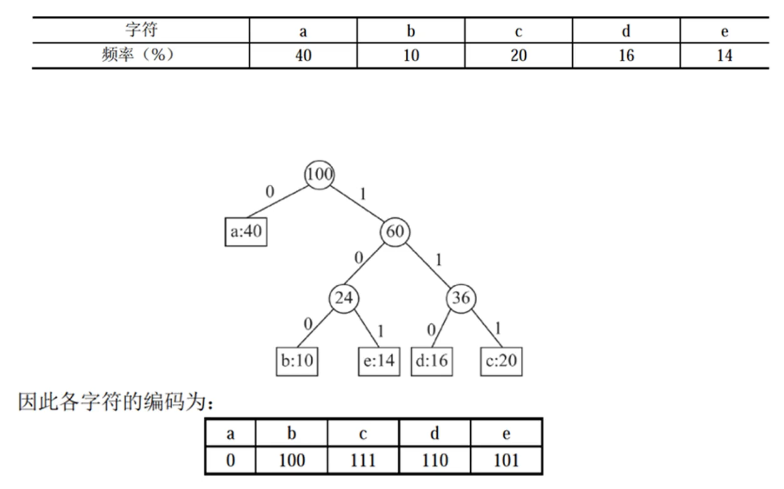
1. 按照出现频率计算加权平均长度：

   $$ 加权平均长度 = \sum_{i=1}^{5}{字符i的位数 \times 字符i出现频率} $$

   即：

   $$ 1 \times 40% + 3 \times (10% + 20% + 16% + 14%) = 2.2 $$

   压缩后平均长度为2.2。

2. 计算压缩比：

   $$ 压缩比 = \cfrac{压缩前编码长度 - 压缩后平均长度}{压缩前编码长度} $$

   即，

   • 编码5个字符至少需要3位：$2^2 < 5 < 2^3$，所以压缩前编码长度为3；

   • 压缩比：

     $$ \cfrac{3-2.2}{3} \approx 0.27 $$

哈夫曼编码方案是基于贪心策略的。

---

图

在图中，任意两个结点之间都可能有直接的关系，所以图中一个结点的前驱结点和后继结点的数目是没有限制的。

图$G$是由集合$V$和$E$构成的二元组，记作$G=(V,E)$：

• 顶点：表示数据元素。$V$是图中顶点的非空有限集合。
• 边：表示数据元素之间的关系。$E$是图中边的有限集合。

图可分为两种类型：

• 有向图：有向图顶点之间的关系称为弧（或有向边），用$<v_i,v_j>$表示，$v_i$是弧尾（始点或起点），$v_j$是弧头（终点，箭头指向的顶点），即有向边是指从弧尾指向弧头的一条边。$<v_i,v_j>$和$<v_j,v_i>$分别表示的是两条边。
• 无向图：无向图顶点之间的关系用$(v_i,v_j)$表示。$(v_i,v_j)$和$(v_j,v_i)$表示的是同一条边。

术语

完全图

完全图：

• 无向完全图：指一个有$n$个顶点的无向图，其每一个顶点与其他$n-1$个顶点之间都有边。

  $n$个顶点的无向完全图共有$\cfrac{n(n-1)}{2}$条边：

  $$ \sum_{i=1}^{n}{i} = \cfrac{n(n-1)}{2} $$

  假设$n$个顶点的无向完全图，为他们编上1到$n$的编号，按照编号顺序计算边，第1个顶点跟其他$n-1$个顶点有$n$条边；第2个顶点跟其他$n-1$个顶点也有$n$条边，除去1条跟第1个顶点相连的边，有$n-1$条不一样的边；第3个顶点出去2条跟第1和第2个顶点相连的边，有$n-2$条不一样的边……以此类推，得出上方公式。

• 有向完全图：指一个有$n$个顶点的有向图，以其每一个顶点为始点与其他$n-1$个顶点之间都有弧。

  $n$个顶点的有向完全图共有$n(n-1)$条边：

  $$ \prod_{i=1}^{n}{n-1} = n(n-1) $$

  有向完全图的$n$个顶点都有$n-1$条以其他顶点作为终点的弧（出度为$n-1$），并且这$n$个顶点的$n-1$条弧都是不同的弧，所以可推出上方公式。

度

度：顶点$v$的度是指关联于该顶点的边的数目，记作$D(v)$。

若为有向图：

• 入度：以该顶点为终点的有向边的数目，记为$ID(v)$；
• 出度：以该顶点为起点的有向边的数目，记为$OD(v)$。

有向图度与入度、出度的关系：

$$ D(v) = ID(v) + OD(v) $$

对于所有的图，顶点数$n$、边数$e$与各顶点的度之间有：

$$ e = \cfrac{1}{2} \sum_{i=1}^{n}{D(v_i)} $$

即，所有顶点的度数之和 $= 2e$。

路径

路径：

• 无向图$G$中的路径：从顶点$v_p$到顶点$v_q$的路径是指存在一个顶点序列$v_p,v_{i1},v_{i2},\cdot,v_{in},v_q$，使得$(v_p,v_{i1}),(v_{i1},v_{i2}),\cdots,(v_{in},v_q) \in E(G)$；

• 无向图$G$中的路径：从顶点$v_p$到顶点$v_q$的路径是指存在一个顶点序列$v_p,v_{i1},v_{i2},\cdot,v_{in},v_q$，使得$<v_p,v_{i1}>,<v_{i1},v_{i2}>,\cdots,<v_{in},v_q> \in E(G)$。

  无向图中的路径也是有方向的。

子图

子图：若有两个图$G=(V,E)$和$G’=(V’,E’)$，如果$V’ \sube V$且$E’ \sube E$，则称$G’$为$G$的子图。

连通图

对于无向图：

• 连通：无向图中，若从顶点$v_i$到顶点$v_j$有路径，则称顶点$v_i$和顶点$v_j$是联通的。
• 连通图：若无向图中任意两个顶点都是联通的，称其为连通图。
• 连通分量：无向图$G$的极大连通子图称为$G$的连通分量。

$n$个结点的连通图，它的边的取值范围是$[n-1,\cfrac{n(n-1)}{2}]$。

对于有向图：

• 强连通图：在有向图$G$中，如果对于每一对顶点，$v_i,v_j\in V$ 且 $v_i \neq v_j$，从顶点$v_i$到顶点$v_j$和从顶点$v_j$到顶点$v_i$都存在路径，则称图$G$为强连通图。
• 强连通分量：有向图中的极大连通子图称为有向图的强连通分量。

连通图是无向图中的一种，所以一般也称为无向连通图。

强连通图是有向图的一种，一般也称为有向强连通图。

网

边（或弧）带权值的图称为网。

有向树

如果一个有向图恰有一个顶点的入度为0（作为root），其余顶点的入度均为1，则是一棵有向树。

基本存储结构

图的基本存储结构有：

• 邻接矩阵表示法：使用矩阵存储顶点关系，适合存储边比较多的图；
• 邻接链表表示法：使用多个单链表存储顶点关系，适合存储边比较少的图。

邻接矩阵表示法

图的邻接矩阵表示法是指用矩阵来表示图中顶点之间的关系。

对于具有$n$个顶点的图$G=(V,E)$，其邻接矩阵是一个$n$阶方阵，且满足：

$$ A[i][j] = \begin{cases} 1 & 若(v_i,v_j)或<v_i,v_j>是E中的边 \\ 0 & 若(v_i,v_j)或<v_i,v_j>不是E中的边 \end{cases} $$

即，横$i$竖$j$，横出竖入。

无向图的邻接矩阵是对称矩阵，有向图的邻接矩阵则不一定对称。

• 无向图：顶点$v_i$的度是邻接矩阵第$i$行（或列）中值不为0的元素个数；
• 有向图：第$i$行的非0元素个数是顶点$v_i$的出度$OD(v_i)$；第$i$列的非0元素个数是顶点$v_i$的入度$ID(v_j)$。

网（赋权图）的邻接矩阵定义（$W_{ij}$是边或弧上的权值）：

$$ A[i][j] = \begin{cases} W_{ij} & 若(v_i,v_j)或<v_i,v_j> \in E \\ \infin & 若(v_i,v_j)或<v_i,v_j> \notin E \end{cases} $$

邻接矩阵适合用于存储边比较多的图。

邻接链表表示法

邻接链表表示法指的是为图的每个顶点建立一个单链表：

• 边结点（表结点）：

  adjvex

  nextarc

  info

  • adjvex：指示与顶点$v_i$邻接的顶点的序号；
  • nextarc：指示下一条边或弧的结点；
  • info：存储与边或弧有关的信息，如权值等。

• 表头结点（顶点结点）：

  data

  firstarc

  • data：存储顶点$v_i$的名或其他有关信息；
  • firstarc：指示链表中的第一个结点（邻接顶点）。

  表头结点通常以顺序存储结构存储，以便随机访问。

对于有向图，邻接链表存储的是以当前结点作为起点的弧；逆邻接链表存储的是以当前结点作为终点的弧。

邻接链表适合用于存储边比较少的图。

遍历

图的遍历是指从某个项点出发，沿着某条搜索路径对图中的所有项点进行访问且只访问一次的过程。

深度优先搜索

深度优先搜索（Depth First Search，DFS）类似于树的先序遍历。从图$G$中任一结点$v$出发按深度优先搜索法进行遍历的步骤：

1. 设置搜索指针$p$，使$p$指向顶点$v$；
2. 访问$p$所指顶点，并使$p$指向与其相邻接的且尚未被访问过的顶点。
3. 若$p$所指顶点存在，则重复步骤2，否则执行步骤4。
4. 沿着访问的次序和方向回溯到最后一个有未被访问过的邻接顶点的顶点，并使$p$指向这个未被访问的顶点，然后重复步骤2到4，直到所有的项点均被访问为止。

时间复杂度（$n$为顶点数，$e$为边数）：

• 邻接矩阵：$O(n^2)$；
• 邻接链表：$O(n+e)$。

广度优先搜索

图的广度优先搜索（Breadth First Search，BFS）步骤为：

1. 从图中的某个顶点$v$出发；
2. 访问$v$后，依次访问$v$的各个未被访问过的邻接点；
3. 分别从$v$的邻接点出发，依次访问它们的邻接点；
4. 按照$v$的邻接点访问的先后顺序，重复步骤2到4，直到图中所有已被访问的项点的邻接点都被访问到；
5. 若此时还有未被访问的顶点，则另选图中的一个未被访问的项点作为起点，重复上述过程，直到图中所有的顶点都被访问到为止。

广度优先搜索可以引入队列来保存已访问过的顶点序列。即，每当一个顶点被访问后，就将其放入队列中；当队头顶点出队时，就访问其未被访问的邻接点并令这些邻接顶点入队。每个顶点最多入队一次。

广度和深度优先搜索遍历图的时间复杂度相同（$n$为顶点数，$e$为边数）：

• 邻接矩阵：$O(n^2)$；
• 邻接链表：$O(n+e)$。

广度和深度优先搜索遍历图的不同之处在于：顶点访问的次序不同。

生成树

连通图的生成树是该图的极小连通子图（都是$n-1$条边）。

对于非连通图而言，每个连通分量中的顶点集和遍历时走过的边集一起构成若干棵生成树，把它们称为非连通图的生成树森林。

• 在图的生成树中任一加一条边，则必然形成回路。

  边数为$e$，$e \ge n$则必然形成回路。

• 图的生成树不是唯一的。

  按深度和广度优先搜索进行遍历将得到不同的生成树，分别称为深度优先生成树和广度优先生成树。

最小生成树

连通网的生成树的边也带权，把生成树各边的权值总和称为生成树的权。权值最小的生成树称为最小生成树。

AOV 网

一个大工程项目可以分为许多较小子工程（称为活动）。有向图中，用顶点表示活动，弧表示活动之间的优先级关系（活动进行时的制约关系），称这样的有向图为以顶点表示活动的网（Activity On Vertex network，AOV网）。

在AOV网中：

• 从顶点$v_i$到$v_j$有一条有向路径：

  • $v_i$是$v_j$的前驱，
  • $v_j$是$v_i$的后继；

• $<v_i,v_j>$：

  • $v_i$是$v_j$的直接前驱，
  • $v_j$是$v_i$的直接后继。

AOV网中不应出现有向环。检测工程是否可行，首先应检查对应AOV网是否存在回路。不存在回路的有向图称为有向无环图（DAG，Directed Acycline Graph）。

拓扑排序

检测AOV网是否是DAG的方法是对AOV网构造其顶点的拓扑有序序列。

拓扑排序是将AOV网中的所有顶点排成一个线性序列的过程，并且该序列满足：若在AOV网中从顶点$v_i$到$v_j$有一条路径，则在该线性序列中，$v_i$必在$v_j$之前。对AOV网进行拓扑排序的方法如下：

1. 在AOV网中选择一个入度为0（没有前驱）的顶点且输出它。
2. 从网中删除该顶点及与该顶点有关的所有弧。
3. 重复上述两步，直到网中不存在入度为0的顶点为止。

两种结果：

• 所有顶点已输出，说明网中不存在回路。
• 尚有未输出的顶点，剩余顶点均有前驱顶点，表面网中存在回路。

有向无环图的拓扑序列中，顶点$v_i$在$v_j$之前，则：

• 可能存在弧$<v_i,v_j>$，一定不存在弧$<v_j,v_i>$；
• 可能存在$v_i$到$v_j$的路径，一定不存在$v_j$到$v_i$的路径。

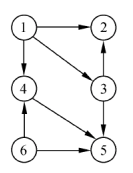
上图拓扑排序的结果为：6,1,4,3,2,5（结果并不唯一）。

当有向图中无环时，也可以利用深度优先遍历进行逆拓扑排序。