计算机系统
跳转连接:软件设计师——计算机系统篇
基本单位
| 位(比特) 最小数据单位 |
bit、b | |
| 字节 最小存储单位 |
byte、B | 1B = 8b |
| 千字节 | KB | 1KB = 1024B |
| 兆字节 | MB | 1MB = 1024KB |
| 吉字节 | GB | 1GB = 1024MB |
| 太字节 | TB | 1TB = 1024GB |
中央处理单元
CPU的功能:
| 功能 | 说明 |
|---|---|
| 程序控制 | 通过执行指令来控制程序的执行顺序。 |
| 操作控制 | CPU产生每条指令的(若干)操作信号并将操作信号送往对应的部件,控制相应的部件按指令的功能要求进行操作。 |
| 时间控制 | 对各种操作进行时间上的控制,即指令执行过程中操作信号的出现时间、持续时间及出现的时间顺序都需要进行严格控制。 |
| 数据处理 | 通过对数据进行算术运算及逻辑运算等方式进行加工处理,数据加工处理的结果被人们所利用。 |
CPU的组成:
- 运算器:
- 算术逻辑单元(ALU):处理数据,对数据进行算术运算和逻辑运算。
- 累加寄存器(AC,累加器):通用寄存器,存放操作数或者结果。。
- 数据缓冲寄存器(DR):暂存由内存读/写的一条指令或一个数据字。
- 状态条件寄存器(PSW):保存了当前指令执行完成之后的状态。
- 控制器:
- 指令寄存器(IR):暂存要执行的指令。
- 程序计数器(PC,指令计数器):寄存信息和指令计数。
- 地址寄存器(AR):保存当前CPU所访问的内存单元的地址。
- 指令译码器(ID)。
- 寄存器组
- 内部总线
数据编码

寻址方式
| 寻址方式 | 说明 |
|---|---|
| 立即寻址 | 操作数就包含在指令中。 |
| 直接寻址 | 操作数在内存,指令给出操作数的地址。 |
| 寄存器寻址 | 操作数在寄存器,指令给出操作数的寄存器名(地址)。 |
| 寄存器间接寻址 | 操作数在内存,寄存器存放操作数的地址,指令给出存放操作数地址的寄存器地址。 |
| 间接寻址 | 指令中给出操作数地址(操作数地址在内存中)的地址。 |
| 相对寻址 | 指令地址码给出的是一个偏移量(可正可负),操作数地址等于本条指令的地址加上该偏移量。 |
| 变址寻址 | 操作数地址等于变址寄存器的内容加偏移量。 |
校验码
编码系统的码距:
- $\ge 2$:该编码系统具有检错能力;
- $\ge 3$:该编码系统才可能有纠错能力。
奇偶校验码:
- 码距为2。
- 仅能检测奇数位数出错。
海明码:
设数据位是$n$位,校验位是$k$位,则$n$和$k$必须满足以下关系:
$$ 2^k-1 \ge n+k $$
循环冗余(n,k)码:
- 信息码(数据),占k位;
- 校验码,占n-k位;
- 码距为2,可以检错不能纠错。
计算机指令集
| RISC 精简指令集(计算机) |
CISC 复杂指令集(计算机) |
|
|---|---|---|
| 指令种类 | 少、精简 | 多、复杂 |
| 指令复杂度 | 低(简单) | 高(复杂) |
| 指令长度 | 固定 | 变化 |
| 寻址方式 | 少 | 复杂多样 |
| 实现(译码方式) | 硬布线控制逻辑(组合逻辑控制器) | 微程序控制技术 |
| 通用寄存器数量 | 多、大量 | 一般 |
| 流水线技术 | 支持 | 不支持 |
流水线技术
执行$n$条指令:
-
顺序执行总时间:
$$ 顺序执行总时间=单条指令执行的时间\times n $$
-
流水线执行总时间:
$$ 流水线执行总时间=一条指令执行的时间+流水线周期 \times (n-1) $$
流水线(操作)周期为执行时间最长的一段操作的时间。
-
连续输入$n$条指令的吞吐率:
$$ 吞吐率=\cfrac {n}{总执行时间} $$
如果是流水线的吞吐率,则总执行时间为流水线执行总时间。 流水线的吞吐率是最长流水段操作时间的倒数。即:
$$ 最长流水段操作时间=\cfrac {流水线执行总时间}{n} $$
-
加速比:
$$ 加速比 = \cfrac{顺序执行总时间}{流水线执行总时间} $$
存储器
按存储器所处位置可分为:
- 内存(主存):在主机内或主板上,存放机器当前运行所需的程序和数据,以便向CPU提供信息。(相对外存)容量小、速度快。
- 外存(辅存):存放当前不参加运行的大量信息,在需要时调入内存。
按存储器工作方式:
- 读/写存储器(RAM)。
- 只读存储器:ROM、PROM、EPROM、EEPROM等。
- 固定只读存储器(ROM):厂家生产时就写好数据在其中。只能读(用户)不能写。一般用于存放BIOS和微程序控制。
- 可编程读只读存储器(PROM):其内容可以由用户一次性地写入,写入后不能再修改。
缓存
高速缓存中的地址映像方法:
-
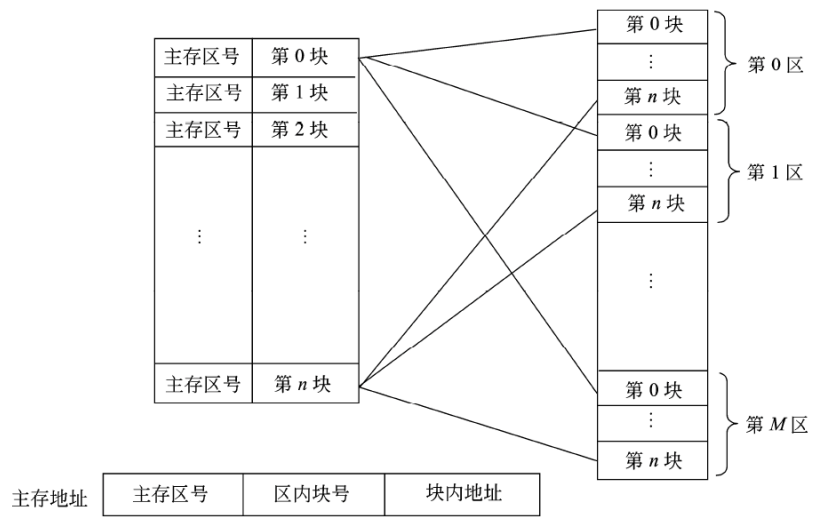
直接映像:主存的块与Cache块的对应关系是固定的。冲突多、关系固定。
-
全相联映像:允许主存的任一块调入Cache存储器的任一块。冲突少、关系不固定。

-
组相联映像:将缓存和主存先分为组,组下再分为块。组与组采用直接映像,组内的块采用全相联映像。冲突较少,是直接映像与全相联映像的折中。
发生块冲突从多到少的顺序:直接映像 > 组相联映像 > 全相联映像。
地址映像都是由硬件自动完成。
中断
程序查询方式(程序直接控制方式):
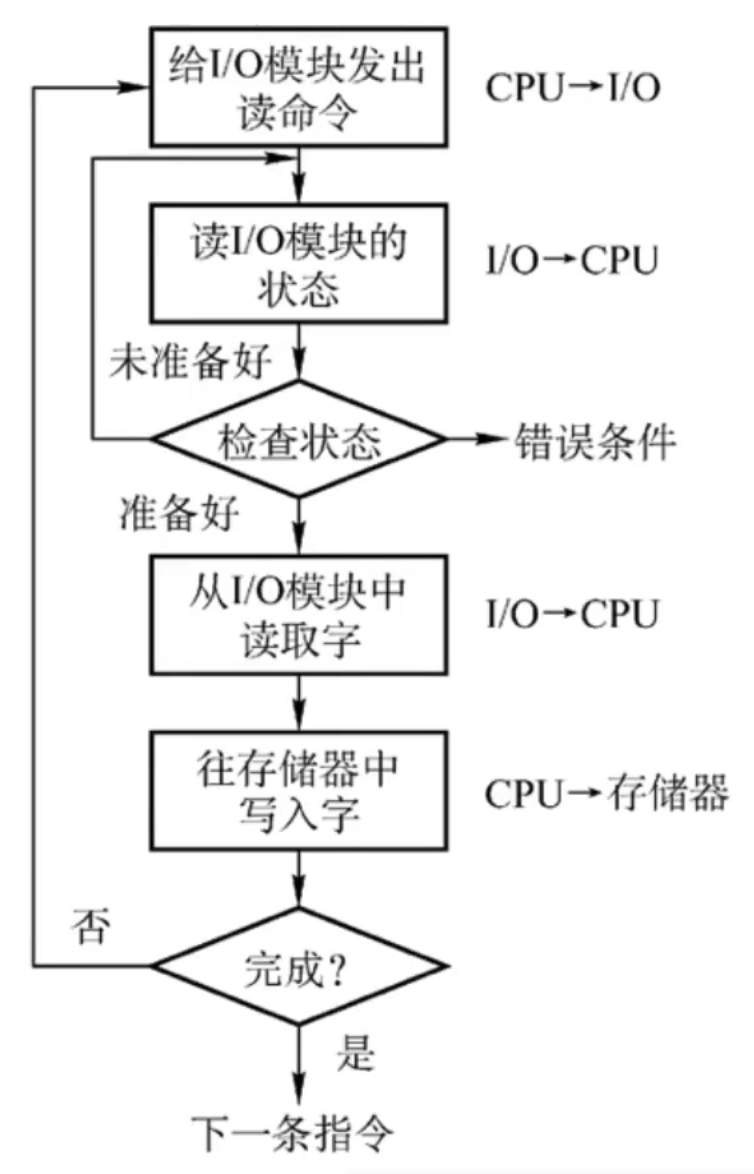
- CPU和I/O只能串行工作。CPU需要一直轮询检查,长期处于忙等状态,CPU利用率低。
- 一次只能读/写一个字。
- 由CPU将数放入内存。
中断驱动方式:

- I/O设备通过中断信号主动向CPU报告I/O操作已完成。
- CPU和I/O可并行工作。
- CPU利用率得到提升。
- 一次只能读/写一个字。
- 由CPU将数据放入内存。
DMA方式(直接存储器存储方式):
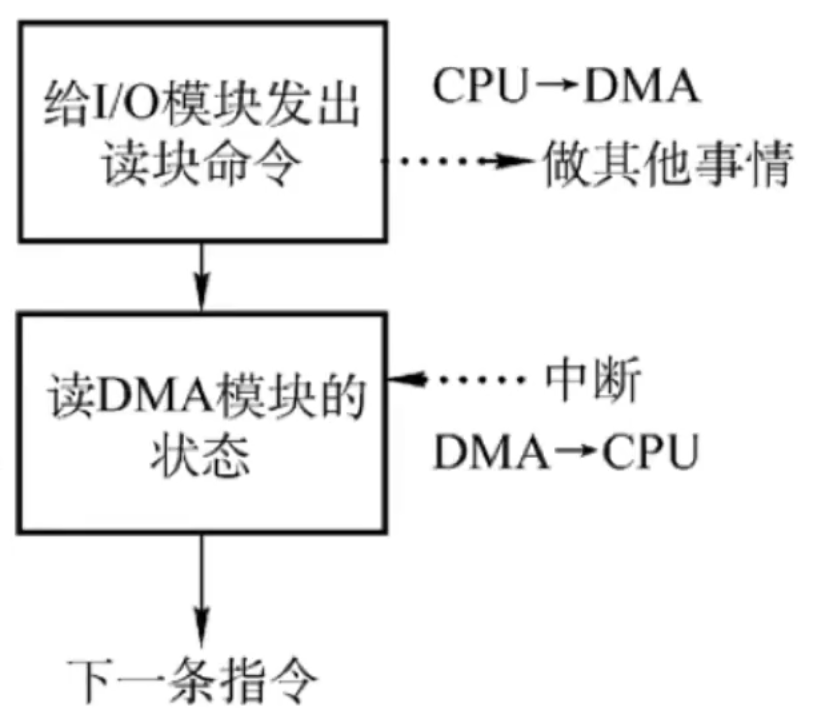
- CPU和I/O可并行工作。
- 仅在传送数据块多开始和结束时才需要CPU的干预。
- 由外设直接将数据放入内存。
- 一次读写的单位为"块"而不是字。
DMA传输数据比中断驱动方式传输数据要快一点。
总线
微机中的总线分为:
- 数据总线
- 地址总线
- 控制总线
常见总线:
- ISA总线。
- EISA总线。
- PCI总线:PCI总线是目前微型机上广泛采用的内总线,采用并行传输方式。
- PCI Express 总线。
- 前端总线。
- RS-232C。
- SCSI总线:小型计算机系统接口(SCSI)是一条并行外总线。
- SATA。
- USB。
- IEEE-1394。
- IEEE-488总线。
加密与认证技术
加密技术用于防止第三方窃听:
-
对称加密:只有一把密钥。加密和解密用同一把密钥。
- 密钥分发有缺陷。
- 加密解密速度很快。
- 适合加量大量明文数据。
-
非对称加密:
- 加密和解密不是同一把密钥。
- 一共有两把密钥,分别是公钥和私钥。
- 用公钥加密只能用私钥解密,用私钥加密只能用公钥解密。
- 不能通过一把密钥推出另一把密钥。
- 用接收方的公钥加密明文可以实现防止窃听的效果。
- 密钥分发没有缺陷。
- 加密解密速度很慢。
认证技术用于防止篡改、假冒和否认:
- 摘要(防止篡改):Hash算法加密,放在密文后。
- 数字签名(防止假冒和否认):发送方用私钥对摘要进行签名(加密)。接收方用发送方的公钥对数字签名进行验证(解密)。
数字证书:CA机构用私钥对用户的公钥签名(加密)。接收方用CA的公钥验证(解密),从而得到用户的公钥。
加密算法:
- 对称密钥(私钥、私有密钥加密)算法(共享密钥加密算法):
- DES
- 3DES
- RC-5
- IDEA
- AES
- RC4
- 非对称密钥(公钥、公开密钥加密)算法:
- RSA
- ECC
- DSA
- 其他加密算法:
- Hash函数
- SHA-1安全散列算法
- MD5摘要算法
系统可靠度
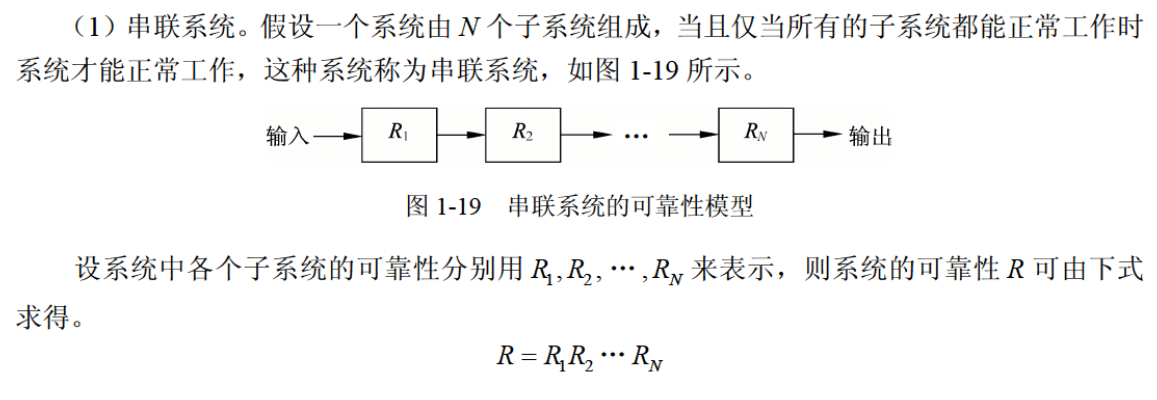

程序设计语言
跳转连接:软件设计师——程序设计语言篇
编译过程
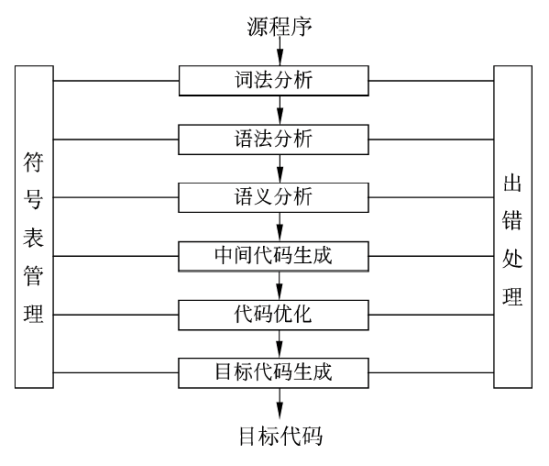
必须的编译过程阶段:
- 词法分析
- 语法分析
- 语义分析
- 目标代码生成
可省略的编译过程阶段:
- 中间代码生成
- (中间或目标)代码优化
| 阶段 | 说明 |
|---|---|
| 词法分析 | 对源程序从前到后(从左到右)逐个字符地扫描,从中识别出一个个“单词”符号 |
| 语法分析 | 根据语言的语法规则将单词符号序列分解成各类语法单位 |
| 语义分析 | 检查源程序是否包含静态语义错误 |
| 中间代码生成 | 分水岭,上面是前端,下面是后端 |
| 代码优化 | 所做的优化一般与具体的机器无关 |
| 目标代码生成 | 把中间代码变换成机器指令 |
正规式
| 符号 | 名称 | 含义 |
|---|---|---|
* |
闭包 | 表示其前面链接的符号或集合可以出现$[0, +\infty]$次。 |
· |
连接 | 可省略,将多个符号或集合连接起来。表示逻辑与 |
| |
或 | 表示逻辑或。 |
Example:
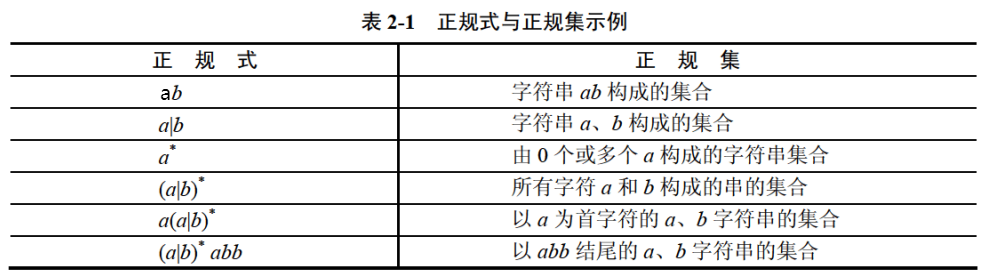
设$U$、$V$和$W$均为正规式:

有限自动机
-
确定的有限自动机(Deterministic Finite Automata,DFA):对每一个状态来说识别字符后转移的状态是唯一的。
一个DFA是一个五元组$(S, \Sigma, f, s_0, Z)$:
-
$S$:包含状态的有限集(每个元素称为一个状态)。
-
$\Sigma$:有穷字母表,其每个元素称为一个输入字符。
-
$f$:$S \times \Sigma \to S$ 上的单值部分映像。
$$ f(A,a)=Q \qquad A \in S, a \in \Sigma $$
表示当前状态为$A$、输入为$a$时,将转换到下一状态$Q$,称$Q$为$A$的一个后继状态。
-
$s_0$:唯一的开始状态,$s_0 \in S$。
-
$Z$:非空的终止状态集合,$Z \subseteq S$。
DFA可以用两种直观的方式表示:
-
状态转换图:简称为转换图,是一个有向图。
-
DFA中的每个状态对应转换图中的一个结点。
-
DFA中的每个转换函数对应图中的一条有向弧。
-
双圈表示的结点是终态结点。
终态也可以是初态。
若转换函数为$f(A,a)=Q$,则该有向弧从结点$A$出发,进入结点$Q$,字符$a$是弧上的标记。
-
-
状态转换矩阵:用一个二位数组$M$表示。
矩阵元素$M[A,a]$:
- 行下标:表示状态。当前状态为$A$。
- 列下标:表示输入的字符。当前输入为$a$。
- $M[A,a]$的值:当前状态为$A$、输入为$a$时,应该转换到的下一状态。


-
-
不确定的有限自动机(Nondeterministic Finite Automata,NFA):对每一个状态来说识别字符后转移的状态是不唯一的。
NFA也是一个五元组$(S, \Sigma, f, s_0, Z)$。与DFA的区别是:
-
$f$是$S \times \Sigma \to 2^S$ 上的映像。
对于$S$中的一个给定状态及输入符号,返回一个状态的集合。即当前状态的后继状态不一定是唯一的。
-
有向弧上的标记可以是 $\varepsilon$($\varepsilon$ 表示空)。
DFA是NFA的特例。
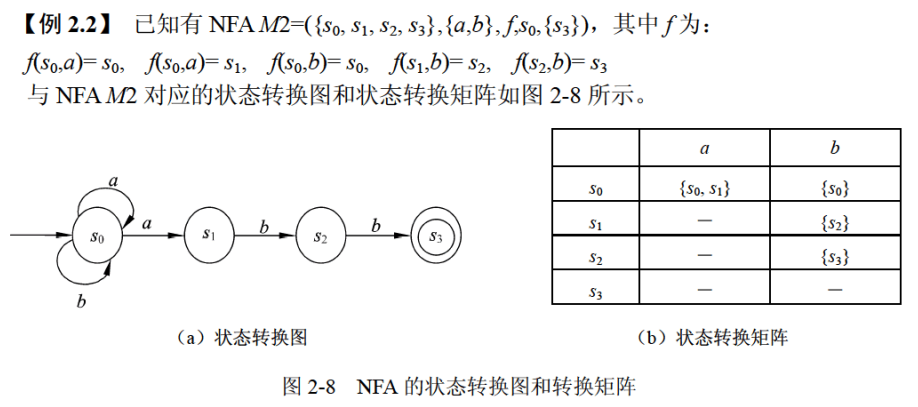
-
有限自动机识别成功的依据是路跑的通并且跑完后的终点是终态。
设计语言成分
| 成分 | 包含 |
|---|---|
| 数据成分 |
|
| 运算成分 |
|
| 控制结构 |
|
| 传输成分 | |
| 函数 |
数据结构
跳转连接:软件设计师——数据结构篇
线性表
顺序表:
在表长为$n$的线性表中,有$n+1$个插入位置(不考虑插入是否会导致溢出):
-
在第$i$个插入位置插入,需要移动$n+1-i$个元素。
- 在第1个位置插入($a_1$)需要移动$n$个元素;
- 在第$n+1$个位置插入($a_n$后面)不需要移动元素。
-
设在第$i$个插入位置插入的概率为$p_i$,等概率下插入一个新元素需要移动的元素个数的期望值$E_{insert}$为:
$$ E_{insert} = \cfrac{插入位置数-1}{2} = \cfrac{n+1}{2} $$
在表长为$n$的线性表中删除元素时,共有$n$个可删除的元素:
-
删除第$i$个元素$a_i$需要移动$n-i$个元素。
- 删除元素$a_1$需要移动$n-1$个元素;
- 删除元素$a_n$不需要移动元素。
-
设$a_i$被删除的概率为$q_i$,等概率下删除元素时需要移动的元素个数的期望值$E_{delete}$为:
$$ E_{delete} = \cfrac{删除位置数}{2} = \cfrac{n-1}{2} $$
插入操作时间复杂度:
- 最好情况(在第$n+1$个位置插入):$O(1)$;
- 最坏情况(在第1个位置插入):$O(n)$;
- 平均复杂度:$O(n)$。
链表插入和删除操作时间复杂度(带不带头节点的复杂度都一样):
- 最好情况(在$i=1$位置):$O(1)$;
- 最坏情况(在$n+1$位置插入/删除$n$位置):$O(n)$
- 平均复杂度:$O(n)$
串的模式匹配
朴素的模式匹配(布鲁特一福斯)算法:
设主串和模式串的长度分别为$n$和$m$,算法时间复杂度和比较次数:
-
最好情况:$O(m)$,次数为$m$;
-
最坏情况:$O(n \times m)$,次数为$\cfrac{1}{2} m(n-m+2)$:
$$ \sum_{i=0}^{n-m}{p_i\big( (i+1) \times m \big)} = \cfrac{m}{n-m+1} \sum_{i=0}^{n-m}{(i+1)} = \cfrac{1}{2} m(n-m+2) $$
-
平均:$O(n+m)$,次数为$\cfrac{1}{2} (n+m)$:
$$ \sum_{i=0}^{n-m}{p_i(i+m)} = \cfrac{1}{n-m+1} \sum_{i=0}^{n-m}{i+m} = \cfrac{1}{2} (n+m) $$
数组
设:
- 二维数组为$A[n,m]$,$n$为行数,$m$为列数;
- 数组元素$a_{i,j},\ 0 \le i \le n-1,\ 0 \le j \le m-1$;
- $LOC(a_{i,j})$为元素$a_{i,j}$的地址;
- $L$为单个元素的存储空间大小。
则有:
-
以行为主序优先存储:
$$ LOC(a_{i,j}) = LOC(a_{0,0}) + (i \times n + j) \times L $$
如果下标从1开始($1 \le i \le n,\ 1 \le j \le m$):
$$ LOC(a_{i,j}) = LOC(a_{1,1}) + \big( (i-1) \times n + (j-1) \big) \times L $$
-
以列为主序优先存储:
$$ LOC(a_{i,j}) = LOC(a_{0,0}) + (i + j \times m) \times L $$
如果下标从1开始($1 \le i \le n,\ 1 \le j \le m$):
$$ LOC(a_{i,j}) = LOC(a_{1,1}) + \big( (i-1) + (j-1) \times m \big) \times L $$
对称矩阵:
假设将$n$阶对称矩阵$A_{n \times n}$压缩存储到一维数组$B\left[ \cfrac{n(n+1)}{2} \right]$,则$B[k]\ (1 \le k \le \cfrac{n(n+1)}{2})$与矩阵元素$a_{ij}(a_{ji})\ (1 \le i,j \le n)$之间存在一一对应关系(以行为主序):
$$ k = \begin{cases} \cfrac{i(i-1)}{2} + j, & 当\ i \ge j \\ \cfrac{j(j-1)}{2} + i, & 当\ i < j \end{cases} $$
如果下标从0开始(第一个元素为$a_{00}$,$0 \le k \le \cfrac{n(n+1)}{2} - 1$,并且$0 \le i,j \le n-1$):
$$ k = \begin{cases} \cfrac{i(i+1)}{2} + j + 1, & 当\ i \ge j \\ \cfrac{j(j+1)}{2} + i + 1, & 当\ i < j \end{cases} $$
三对角矩阵:
设有$n$阶三对角矩阵$A_{n \times n}$,将其非0元素$a_{ij}(a_{ji})\ (1 \le i,j \le n)$存储在一维数组$B[k](1 \le k \le 3 \times n - 2)$中,则元素位置之间的对应关系为:
$$ k = 3 \times (i-1) - 1 + j - i + 1 + 1 = 2i + j -2 $$
如果下标从0开始($0 \le k \le 3(n-1)$,并且$0 \le i,j \le n-1$):
$$ k = 3 \times i - 1 + j - i + 1 + 1 = 2i + j + 1 $$
树
-
设$n$个结点的树,$d_i \ (1 \le i \le n)$为该树中结点的度:
$$ n = (\sum_{i=1}^{n}{d_i})+1 $$
度:结点拥有的子树数。
-
度为$m$的树中第$i$层上至多有$m^{i-1}$个结点($i \ge 1$)。
-
高度为$h$的$m$度树至多有$\cfrac{m^h-1}{m-1}$个结点。
二叉树:
-
第$i$层($i \ge 1$)上最多有$2^{i-1}$个结点。
-
高度为$k$的二叉树最多有$2^k-1$个结点($k \ge 1$)。
-
若二叉树终端结点数(度为0的结点数)为$n_0$,度2的结点数为$n_2$,则$n_0=n_2+1$。
-
具有$n$个结点的完全二叉树的深度(高度)为:
$$ \lfloor \log_2{n} \rfloor + 1; $$
或:
$$ \lceil \log_2{(n+1)} \rceil $$
-
二叉树形态总数(卡特兰数):
$$ \cfrac{C^{n}_{2n}}{n+1} $$
链式存储二叉树:
设有$n$个结点的二叉树,则其空指针域数量:
-
对于二叉链表:
- 总指针域个数:$2n$;
- 分支数(子孙结点数,非空指针域个数):$n-1$。
可得:
$$ 空指针域数=2n-(n-1)=n+1 $$
-
对于三叉链表:
- 总指针域个数:$3n$;
- 分支数(子孙结点数):$n-1$;
- 指向父结点且非空的指针域个数:$n-1$。
即,非空指针域个数为:$2(n-1)$。
可得:
$$ 空指针域数=3n-2(n-1)=n+2 $$
平衡二叉树:
设一个二叉树的左右子树高度之差的绝对值为$d$,那么
- 不平衡的二叉树:$d > 1$;
- 平衡的二叉树:$d \le 1$。
哈夫曼树(最优二叉树):带权路径长度最短。
设:
- 带权叶子结点数:$n$;
- 叶子结点的权值:$w_k$;
- 叶子结点到根的路径长度:$l_k$。
则树的带权路径长度为:
$$ WPL = \sum_{k=1}^{n}{w_kl_k} $$
给定$n$个权值后,哈夫曼树的结点数$m$就确定了:
$$ m = 2 \times n - 1 $$
哈夫曼压缩比:
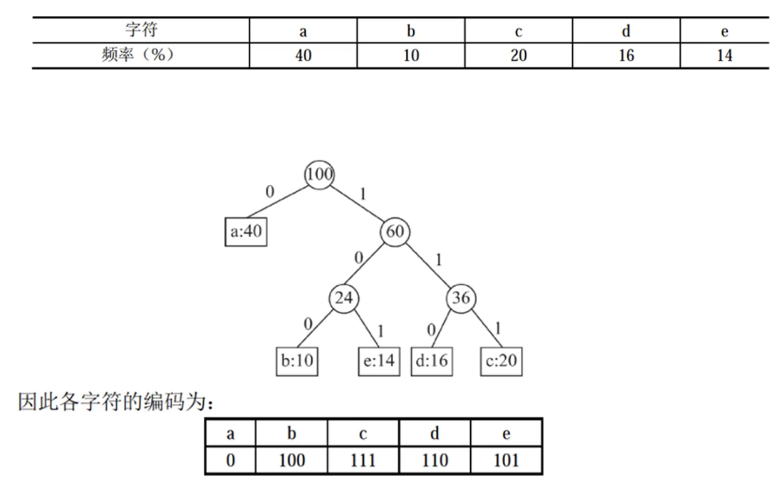
-
按照出现频率计算加权平均长度:
$$ 加权平均长度 = \sum_{i=1}^{5}{字符i的位数 \times 字符i出现频率} $$
即:
$$ 1 \times 40% + 3 \times (10% + 20% + 16% + 14%) = 2.2 $$
压缩后平均长度为2.2。
-
计算压缩比:
$$ 压缩比 = \cfrac{压缩前编码长度 - 压缩后平均长度}{压缩前编码长度} $$
即,
-
编码5个字符至少需要3位:$2^2 < 5 < 2^3$,所以压缩前编码长度为3;
-
压缩比:
$$ \cfrac{3-2.2}{3} \approx 0.27 $$
-
图
完全图:
- $n$个顶点的无向完全图共有$\cfrac{n(n-1)}{2}$条边。
- $n$个顶点的有向完全图共有$n(n-1)$条边。
对于所有的图,其所有顶点的度数之和 $= 2e$($e$为边数)。
$n$个结点的连通图,它的边的取值范围是$[n-1,\cfrac{n(n-1)}{2}]$。
图的邻接矩阵:横$i$竖$j$,横出竖入。
深度优先搜索:
- 设置搜索指针$p$,使$p$指向顶点$v$;
- 访问$p$所指顶点,并使$p$指向与其相邻接的且尚未被访问过的顶点。
- 若$p$所指顶点存在,则重复步骤2,否则执行步骤4。
- 沿着访问的次序和方向回溯到最后一个有未被访问过的邻接顶点的顶点,并使$p$指向这个未被访问的顶点,然后重复步骤2到4,直到所有的项点均被访问为止。
广度优先搜索:
- 从图中的某个顶点$v$出发;
- 访问$v$后,依次访问$v$的各个未被访问过的邻接点;
- 分别从$v$的邻接点出发,依次访问它们的邻接点;
- 按照$v$的邻接点访问的先后顺序,重复步骤2到4,直到图中所有已被访问的项点的邻接点都被访问到;
- 若此时还有未被访问的顶点,则另选图中的一个未被访问的项点作为起点,重复上述过程,直到图中所有的顶点都被访问到为止。
广度和深度优先搜索时间复杂度(一样):
- 邻接矩阵:$O(n^2)$;
- 邻接链表:$O(n+e)$。
AOV 网拓扑排序:如果所有顶点已输出,说明网中不存在回路,否则说明存在。
- 在AOV网中选择一个入度为0的顶点且输出它。
- 从网中删除该顶点及与该顶点有关的所有弧。
- 重复上述两步,直到网中不存在入度为0的顶点为止。
操作系统
跳转连接:软件设计师——操作系统篇
进程的三态
- 运行:当一个进程在处理机上运行时。
- 就绪:一个进程获得了除处理机外的一切所需资源,一旦得到处理机即可运行(还未得到)。
- 阻塞(等待或睡眠):一个进程正在等待某一事件发生而暂时停止运行,这时即使把处理机分配给进程也无法运行。
同步互斥
-
同步:指在系统中一些需要相互合作,协同工作的进程。
-
互斥:指系统中多个进程因争用临界资源而互斥执行。
-
临界资源(CR):在多道程序系统环境中,那些一次只能供一个进程使用的资源。如打印机、共享变量和表格等。
-
临界区(CS):是进程中对临界资源实施操作的那段程序。
互斥临界区管理的4条原则:有空即进、无空则等、有限等待和让权等待。
信号量
- 公用信号量:实现进程间的互斥,初值为
1或资源的数目。 - 私用信号量:实现进程间的同步,初值为
0或某个正整数。
信号量$S$的物理意义:
- $S \ge 0$:表示某资源的可用数,此时有可用资源;
- $S < 0$:则其绝对值表示阻塞队列中等待该资源的进程数,此时无可用资源,并且有进程被阻塞。
PV操作:P申请V释放,P减V加,P进V出。
- P操作$S < 0$:无可用资源,置该进程为阻塞状态。
- V操作$S \le 0$:表示释放前有程序被阻塞,从阻塞状态唤醒一个进程,并将其插入就绪队列。
假定信号量S表示某条消息,进程可以:
- 调用P操作:测试消息是否到达;
- 调用V操作:通知消息已经准备好。
死锁
产生死锁的原因:
- 进程间互相竞争资源。
- 进程推进顺序非法。
产生死锁的4个必要条件:
- 互斥条件
- 请求保持条件
- 不可剥夺条件
- 环路条件
发生死锁时,在进程资源有向图中必构成环路。
造成死锁的情况:
- 进程推进顺序不当
- 同类资源分配不当
- PV操作使用不当
死锁的处理策略:
- 鸵鸟策略(不理睬策略)
- 预防策略
- 避免策略
- 检测与解除死锁
死锁预防:
-
预先静态分配法:破坏了“不可剥夺条件”,预先分配所需资源,保证不等待资源。
该方法的问题是降低了对资源的利用率,降低进程的并发程度;有时可能无法预先知道所需资源。
-
资源有序分配法:破坏了“环路条件”,把资源分类按顺序排列,保证不形成环路。
该方法存在的问题是限制进程对资源的请求:由于资源的排序占用系统开销。
线程(轻型进程)
- 基本上不拥有资源,只拥有一点运行中必不可少的资源(如程序计数器、一组寄存器和栈)。
- 与其它同一进程的线程共享进程所拥有的全部资源。
线程分为:
- 用户级线程
- 内核支持线程
存储管理
程序的局限性:
-
时间局限性:
- 如果程序中的某条指令一旦执行,则不久的将来该指令可能再次被执行;
- 如果某个存储单元被访问,则不久以后该存储单元可能再次被访问。
产生时间局限性的典型原因是在程序中存在着大量的循环操作。
-
空间局限性:指一旦程序访问了某个存储单元,则在不久的将来,其附近的存储单元也最有可能被访问。
即程序在一段时间内所访问的地址可能集中在一定的范围内,其典型原因为程序是顺序执行的。
段页式存储管理:
- 将整个主存划分成大小相等的存储块(页框)。
- 将用户程序按程序的逻辑关系分为若干个段,并为每个段赋予一个段名。
- 将每个段划分成若干页,以页框为单位离散分配。
缓冲
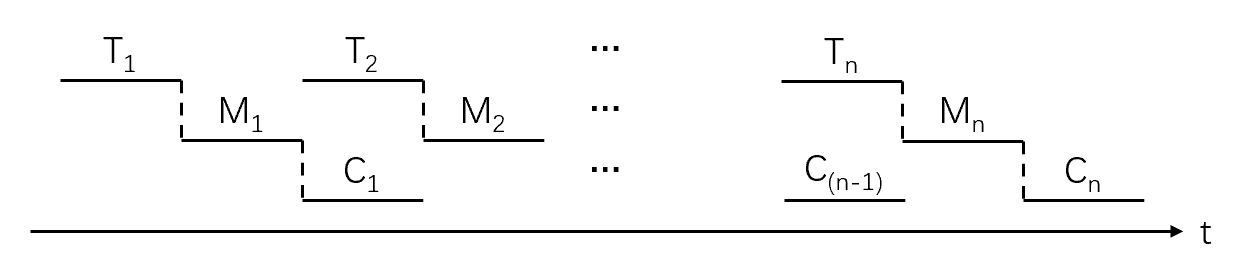
$n$个作业的单缓冲所花费的时间为:
$$ (Max(C, T) + M) \times n + Min(C, T) $$
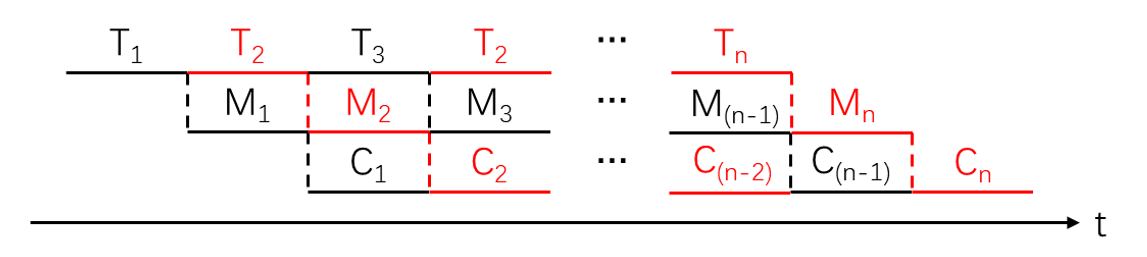
$n$个作业的双缓冲所花费的时间为:
$$ Max(T, M, C) \times n + T + M + C - Max(T, M, C) $$
即,
$$ Max(T, M, C) \times (n - 1) + T + M + C $$
磁盘调度
-
先来先服务(First-Come First-Served,FCFS):根据进程请求访问磁盘的先后次序进行调度。
- 优点:公平、简单,且每个进程的请求都能依次得到处理,不会出现某进程的请求长期得不到满足的情况。
- 缺点:此算法由于未对寻道进行优化,致使平均寻道时间可能较长。
-
最短寻道时间优先(Shortest Seek Time First,SSTF,最短移臂算法):该算法选择这样的进程,其要求访问的磁道与当前磁头所在的磁道距离最近,使得每次的寻道时间最短。
- 优点:可能会出现饥饿现象。
- 缺点:不能保证平均寻道时间最短。
-
扫描算法(SCAN,电梯调度算法):总是从磁头当前位置开始,沿磁头的移动方向去选择离当前磁头最近的那个柱面的请求。如果沿磁头的方向无请求访问时,就改变磁头的移动方向。
在这种调度方法下磁头的移动类似于电梯的调度,所以它也称为电梯调度算法。
- 优点:避免了饥饿现象的出现。
- 缺点:当磁头刚从里向外移动过某一磁道时,恰有一进程请求访问此磁道,这时该进程必须等待,待磁头从里向外,再从外向里扫描完所有要访问的磁道后才处理该进程的请求,致使该进程的请求被严重地推迟。
-
单向扫描算法(CSCAN,循环扫描算法):为了减少上述SCAN缺点中存在的这种延迟,算法规定磁头只做单向移动。
例如,只是自里向外移动,从当前位置开始沿磁头的移动方向去选择离当前磁头最近的那个柱面访问,如果沿磁头的方向无请求访问时,磁头立即返回到最里面的欲访问的柱面,再亦即将最小柱面号紧接着最大柱面号构成循环,进行循环扫描。
旋转调度算法
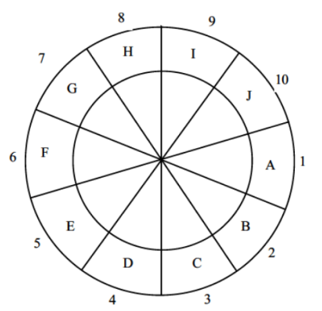
设$n$个扇区的磁盘,经过一个扇区的时间为$t$,读取一个记录后处理的时间为$c$,那么:
-
顺序处理完所有记录的总时间为:
$$ (t + nt) (n-1) + t + c $$
即:
$$ t \times n^2 + c $$
-
记录优化后的总时间:
$$ n(t + c) $$
多级磁盘索引结构
-
直接索引:索引表中的地址项直接指向磁盘数据块。
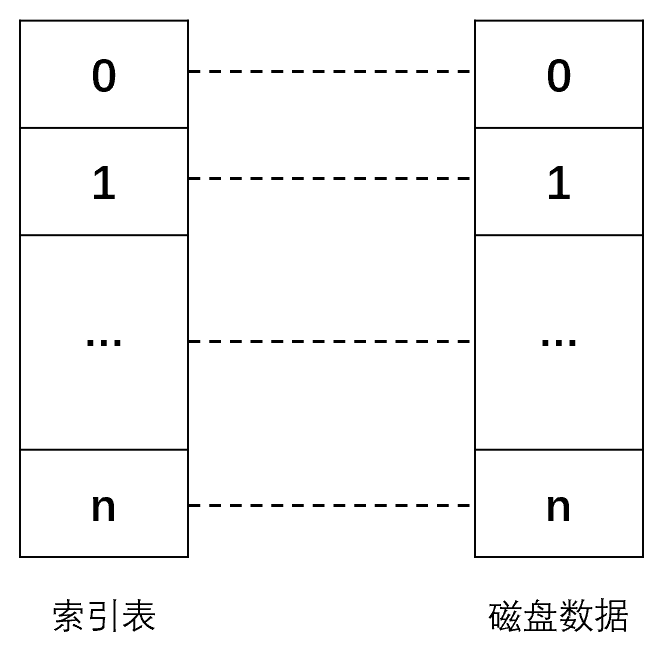
-
一级间接地址索引:索引表中的地址项指向一个磁盘索引块。这个索引块中的记录是地址项,这些地址项直接指向磁盘数据块。
称这个磁盘索引块为一级索引块。
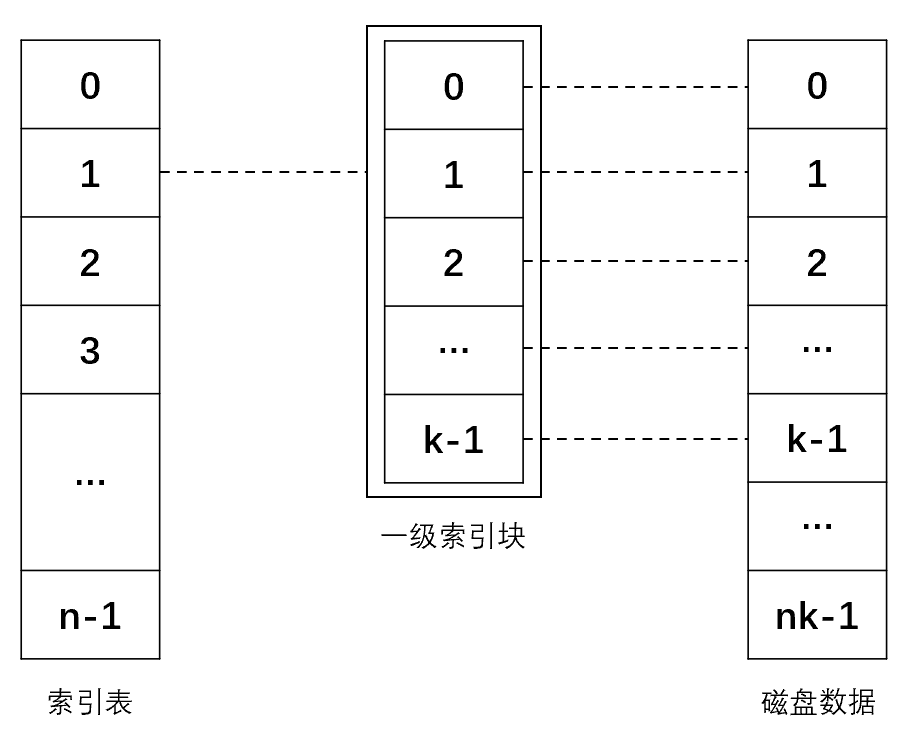
-
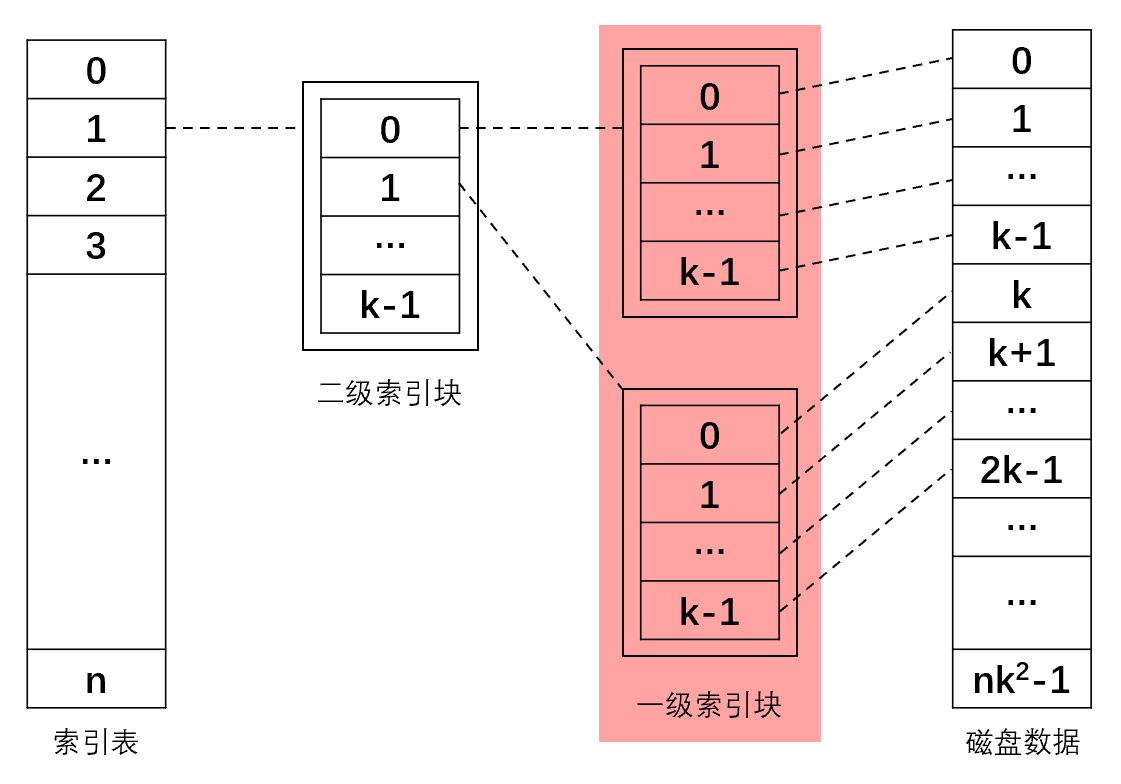
二级间接地址索引:索引表中的地址项指向一个磁盘索引块。这个索引块中的一个记录指向一个一级索引块。
称这个记录指向一级索引块的磁盘索引块为二级索引块。
面向对象
跳转连接:软件设计师——面向对象篇
设计原则
-
责任原则(Single Responsibility Principle,SRP):当需要修改某个类的时候原因有且只有一个,让一个类只做一种类型责任。
-
开放封闭原则(Open & Close Principle,OCP):软件实体(类、模块、函数等)应 该可以扩展的,即开放的;但是不可修改的,即封闭的。
-
里氏替换原则(Liskov Substitution Principle,LSP):子类型必须能够替换掉他们的基 类型。
即,在任何父类可以出现的地方,都可以用子类的实例来赋值给父类型的引用。
当一个子类的实例应该能够替换任何其超类的实例时,它们之间才具有是一个(is-a)关系。
-
依赖倒置原则(Dependence Inversion Principle,DP):抽象不应该依赖于细节,细 节应该依赖于抽象。即,高层模块不应该依赖于低层模块,二者都应该依赖于抽象。
-
接口分离原则(Interface Segregation Principle,ISP):不应该强迫客户依赖于它们不 用的方法。接口属于客户,不属于它所在的类层次结构。
即:依赖于抽象,不要依赖于具体,同时在抽象级别不应该有对于细节的依赖。
这样做的好处就在于可以最大限度地应对可能的变化。
Robert C. Martin提出的面向对象设计原则(重点的):
- 共同封闭原则(Common Closure Principle,CCP):包中的所有类对于同一类性质的变化应该是共同到闭的。一个变化若对一个包产生影响,则将对该包中的所有类产生影响,而对于其他的包不造成任何影响。
- 共同重用原则(Common Reuse Principle,CRP):一个包中的所有类应该是共同重用 的。如果重用了包中的一个类那么就要重用包中的所有类。
UML
| UML图 | 静态建模 | 动态建模 | 物理建模 |
|---|---|---|---|
| 类图 | $\checkmark$ | $\times$ | $\times$ |
| 对象图 | $\checkmark$ | $\times$ | $\times$ |
| 用例图 | $\checkmark$ | $\times$ | $\times$ |
| 构件图(组件图) | $\checkmark$ | $\times$ | $\checkmark$ |
| 部署图 | $\checkmark$ | $\times$ | $\checkmark$ |
| 序列图(顺序图,时序图) | $\times$ | $\checkmark$ | $\times$ |
| 通信图(协作图) | $\times$ | $\checkmark$ | $\times$ |
| 状态图 | $\times$ | $\checkmark$ | $\times$ |
| 活动图 | $\times$ | $\checkmark$ | $\times$ |
活动图是一种特殊的状态图,它们的差异如下:
- 相同点:状态中都有初态和终态。
- 主要差异:
- 活动图的转换称为流;
- 活动图有分支、并发分岔和并发汇合。
顺序图和通信图是同构的,它们之间可以相互转换。它们的差异如下:
| 差异 | ||
|---|---|---|
| 强调 | ||
| 不同的特性 |
|
|
以下是UML图的总结:
-
类图:展现一组对象(类)、接口、协作和它们之间的关系
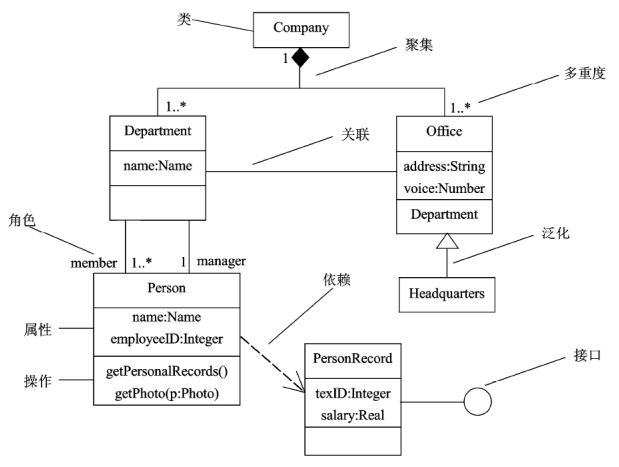
-
对象图:展现某一时刻的一组对象以及它们之间的关系,描述了在类图中所建立事物的实例的静态快照
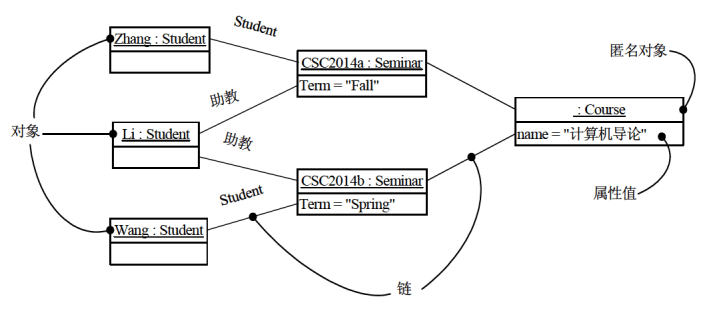
-
用例图:展现了一组用例、参与者以及它们之间的关系(包含、扩展、关联和泛化)
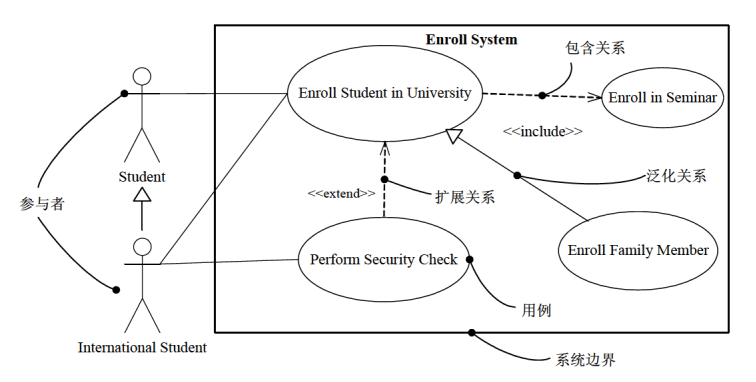
-
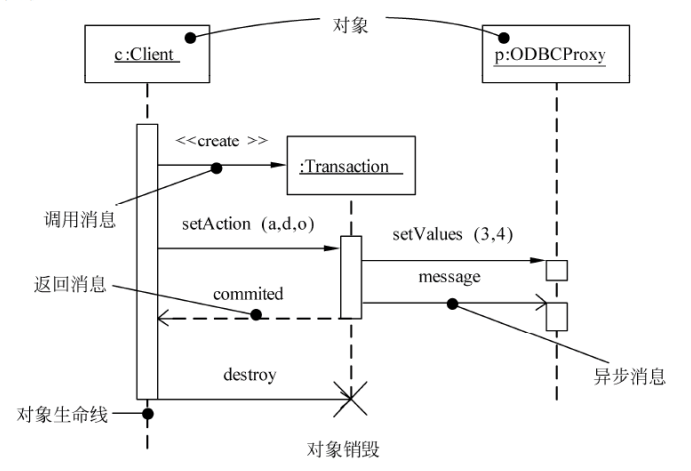
序列图(顺序图,时序图):描述了以时间顺序组织的对象之间的交互活动,强调消息时间顺序
-
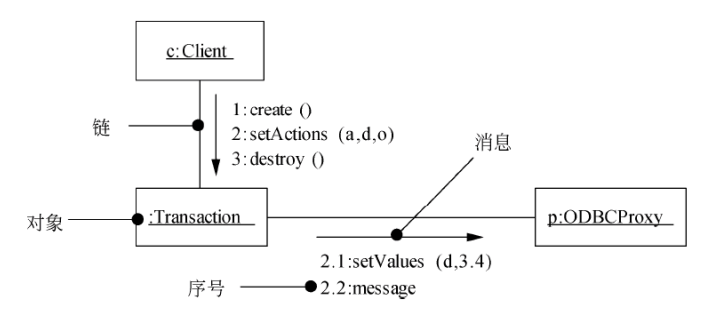
通信图(协作图):强调收发消息的对象的结构组织
-
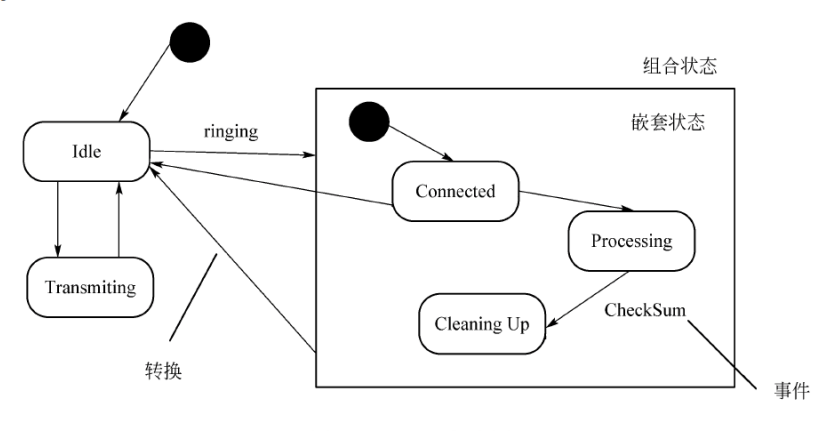
状态图(状态转换图):展现了一个状态机,强调对象行为的事件顺序
-
活动图:一种特殊的状态图,展现了在系统内从一个活动到另一个活动的流程,强调对象间的控制流程
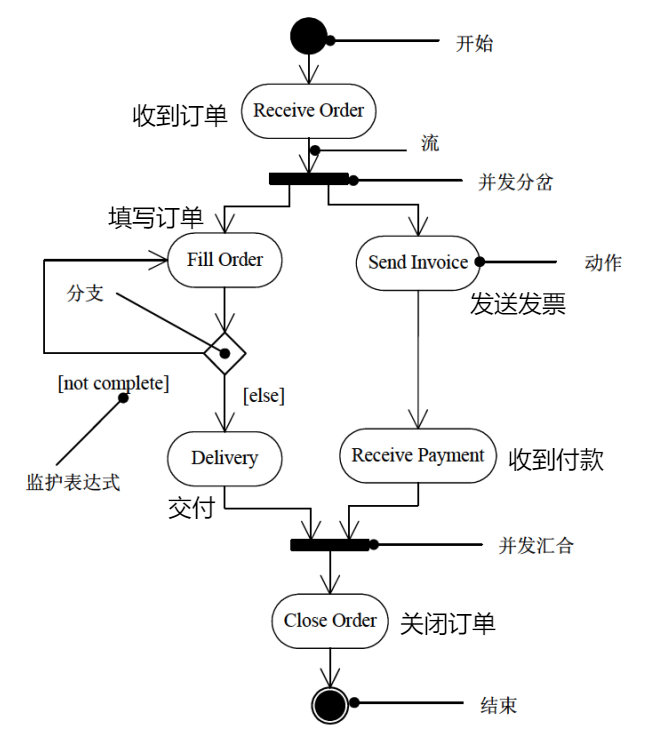
-
构件图(组件图):展现了一组构件之间的组织和依赖,将构件映射为类、接口或协作
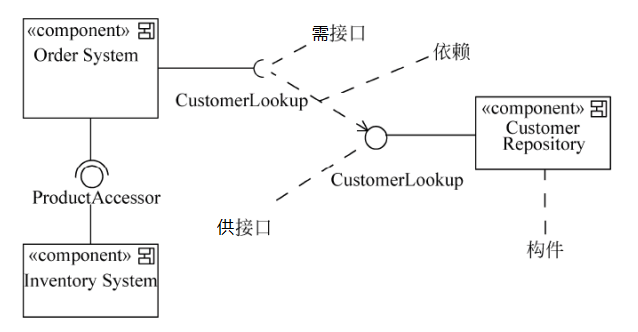
-
部署图:对物理建模,展现了运行时处理结点以及其中构件(制品)的配置
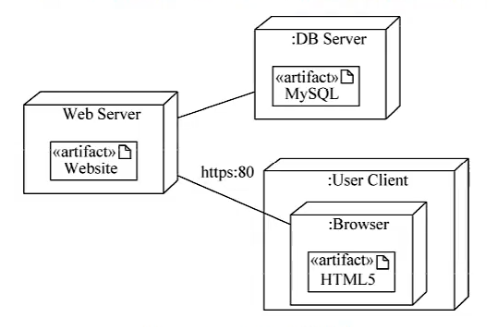
设计模式
设计模式代码仓库:https://gitee.com/linner_cheng/design-patterns
设计模式分类:
| 创建型 | 结构型 | 行为型 | |
|---|---|---|---|
| 说明 | 与对象的创建有关 | 处理类或对象的组合 | 描述类或对象的交互和职责分配 |
| 类模式 | Factory Method(工厂方法模式) | Adapter(适配器模式) | Interpreter(解释器模式) Template Method(模板方法模式) |
| 对象模式 | Abstract Factory(抽象工厂模式) Builder(生成器模式) Prototype(原型模式) Singleton(单例模式) |
Adapter(适配器模式) Bridge(桥接模式) Composite(组合模式) Decorator(装饰器模式) Facade(外观模式) Flyweight(享元模式) Proxy(代理模式) |
Chain of Responsibility(责任链模式) Command(命令模式) Iterator(迭代器模式) Mediator(中介者模式) Memento(备忘录模式) Observer(观察者模式) State(状态模式) Strategy(策略模式) Visitor(访问者模式) |
创建型设计模式(抽象了对象的实例化过程):
| 模式 | 关键字 | 意图 |
|---|---|---|
| 工厂方法 | 动态生产对象 | 定义创建对象的接口,由子类实例化对象。让类的实例化延迟到其子类。 |
| 抽象工厂 | 生成系列对象 | 提供创建一系列对象的接口,无需指定具体的类。 |
| 生成器 | 构造复杂对象 | 将复杂对象的构建与表示分离。使得同样的构建可以创建不同的表示。 |
| 原型 | 克隆对象 | 用原型实例指定创建对象的类型,通过复制原型来创建对象。 |
| 单例 | 一个实例 | 保证一个类仅有一个实例,并提供一个全局访问点。 |
| 模式 | 适用性 |
|---|---|
| 工厂方法 |
|
| 抽象工厂 |
|
| 生成器 |
|
| 原型 |
|
| 单例 |
|
结构型模式(组合类或对象获得新的结构):
| 模式 | 关键字 | 意图 |
|---|---|---|
| 适配器(类/对象) | 接口转换 | 将类的接口转换成兼容其他类的接口。 使原本接口不兼容的类可以一起工作。 |
| 桥接 | 抽象与实现分离 | 将类的抽象与实现分离,使它们可以独立变化。 |
| 组合 | 组合对象 | 将对象组合成树型结构以表示“部分——整体”的层次结构。 使得用户对单个对象和组合对象的使用具有一致性。 |
| 装饰 | 动态附加职责 | 动态地给一个对象添加一些额外的职责,比用子类来扩展功能更灵活。 |
| 外观 | 对外统一接口 | 为子系统定义和提供一个统一的对外高层接口(外观)。 简化了该子系统的使用。 |
| 享元 | 共享大量细粒度对象 | 提供支持大量细粒度对象共享的有效方法。 |
| 代理 | 中介代理 | 为其他对象提供一种代理以控制对这个对象的访问。 |
| 模式 | 适用性 |
|---|---|
| 适配器 |
|
| 桥接 |
|
| 组合 |
|
| 装饰器 |
|
| 外观 |
|
| 享元 |
|
| 代理 |
|
行为型模式:
| 模式 | 关键字 | 意图 |
|---|---|---|
| 责任链 | 职责传递 | 将处理请求的多个对象连成一条链,请求在链中传递,直到有对象处理。 给多个对象处理请求的机会,减少请求的发送者与接收者之间的耦合。 |
| 命令 | 请求封装为对象 | 将一个请求封装为一个对象,可用不同请求对客户进行参数化。 将请求排队或记录日志,支持撤销操作。 |
| 解释器 | 语句解释 | 给定一种语言,定义其文法和解释器,解释器根据文法解释语言中的句子。 |
| 迭代器 | 顺序访问数据集 | 提供一个顺序访问聚合对象中元素的方法,不需要暴露对象的内部表示。 |
| 中介者 | 不直接引用 | 用对象封装一系列的对象交互。 使各对象不需显式地相互调用,达到低耦合。 可以独立改变对象间的交互。 |
| 备忘录 | 保存状态 | 不破坏封装的前提下,捕获对象的内部状态,并在该对象之外保存。 可以在以后恢复保存的状态。 |
| 观察者 | 联动 | 定义对象间的一种一对多依赖关系。 一个对象状态改变,所有依赖于它的对象都得到通知并被自动更新。 |
| 状态 | 状态封装成类 | 把对象的行为封装在不同的状态对象中。 允许一个对象在其内部状态改变时改变它的行为。 |
| 策略 | 多方案切换 | 定义并封装一系列算法,使它们可以在不影响客户端的情况下相互替换。 |
| 模板方法 | 框架 | 定义一个操作中的算法骨架,让其子类来实现算法中的剩余逻辑。 可以不改变算法结构而重新定义其某些特定步骤。 |
| 访问者 | 数据与操作分离 | 封装作用与某对象结构中元素的操作。 可以在不改变元素类的前提下,定义或修改作用于这些元素的操作。 |
| 模式 | 适用性 |
|---|---|
| 责任链 |
|
| 命令 |
|
| 解释器 |
|
| 迭代器 |
|
| 中介者 |
|
| 备忘录 |
|
| 观察者 |
|
| 状态 |
|
| 策略 |
|
| 模板方法 |
|
| 访问者 |
|
个人理解的方式:
| 模式 | 简述 |
|---|---|
| 工厂方法 | 具体工厂(工厂接口的实现)创建具体对象。 |
| 抽象工厂 | 一个具体工厂(抽象工厂的子类)创建多个产品,不同工厂用不同方式创建这一系列产品。 |
| 生成器 | 复杂对象通过切换构建construct(Builder)来创建不同表示。 |
| 原型 | 多个原型之间通过克隆Prototype.clone()来复制对象。 |
| 单例 | 通过私有化无参构造方法、静态Singleton instance属性和静态getInstance()方法使对象保持单例。 |
| 适配器 | 适配器继承目标类,重写目标类的方法,方法将不兼容的接口包装成与目标类一致的接口。 |
| 桥接 | 将产品(抽象)与其某属性(实现)分开,通过桥接(组合)产品与其属性独立出来的类来制造不同产品。 |
| 组合 | 用树形结构和一致的抽象类让部分和整体的操作一致。如文件树。 |
| 装饰器 | 装饰器继承被装饰类,通过构造器传入被装饰对象,然后在与被装饰类一致的方法中添加新操作。多个装饰器嵌套可组成一条装饰链。 |
| 外观 | 复杂子系统有很多操作,外观将其简化。跟适配器很像。 |
| 享元 | 让一个对象假装成许多个对象。就是很多个对象之间可能有一部分属性的值是一样的,定义一个对象然后共享这部分属性。 |
| 代理 | 代理就是给被代理对象加一些操作,跟适配器和外观不同的是代理的接口是与被代理对象一致的。 |
| 责任链 | 有多个接口一致的对象,将请求在这些对象间层层转发,请求可以被其中一个对象处理(JavaWeb里的过滤器)。和嵌套的装饰器很像。 |
| 命令 | 就是一个命令一个对象,调用这些对象的方式一致(对象接口一致)。 |
| 解释器 | 解释语言的上下文。 |
| 迭代器 | 在集合对象的外部,通过迭代器访问集合中的元素,对应的迭代器可由集合对象给出iterator()。跟Java里的迭代器一个样。 |
| 中介者 | 有多个类似对象,这些对象通过中介互相发送消息(就好像微信聊天一样,微信就是中介)。 |
| 备忘录 | 捕获并保存对象的内部状态,并且可以恢复到原型保存的状态。 |
| 观察者 | 在目标对象状态更新时,观察者们可以收到通知update(),然后更新自身状态,与目标对象的状态保持一致。 |
| 状态 | 一个状态一个类,在状态中通过判断变换到其它状态。 |
| 策略 | 就是动态切换算法。 |
| 模板方法 | 模板实现算法操作中不变的部分,其余的交给子类去实现。 |
| 访问者 | 就是在Visitor.visit(访问对象)中定义对象的操作,然后在结构类中提供accept(Visitor)来访问这些对象。 |
数据库
跳转连接:软件设计师——数据库篇
三级模式两级映像
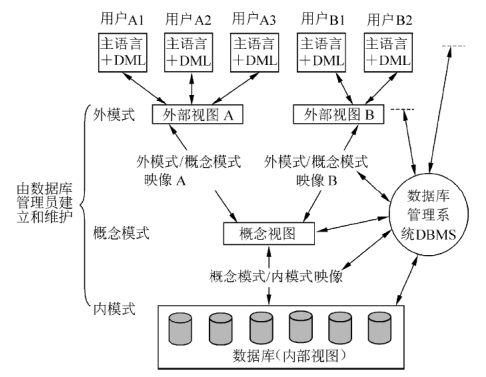
三级结构有3类数据模型:
- 外模型:用户使用的数据视图,是一种局部的逻辑数据视图,表示用户所理解的实体、实体属性和实体关系。
- 概念模型:全局的逻辑数据视图,是数据库管理员所看到的实体、实体属性和实体之间的联系。
- 内模型:数据的物理存储模型。
三个物理模型分别对应数据库系统的3层结构:
-
外模式(子模式、用户模式):数据库用户的数据视图,是与某一应用程序有关的数据的逻辑表示。
-
概念模式(模式):所有用户的公共数据视图,与具体的应用程序和应用程序开发工具无关。
-
内模式(物理模式、存储模式):是数据在数据库内部的表示方式。
定义所有的内部记录类型、索引和文件的组织方式。
数据库系统在三级模式之间提供了两级映像:
- 模式——内模式映像存在于概念级和内部级之间,实现概念模式和内模式间的相互转换。
- 外模式——模式映像:存在于外部级和概念级之间,实现了外模式和概念模式之间的相互转换。
二级映像功能保证数据的独立性:
- 物理独立性:指当数据库的内模式发生改变时,数据的逻辑结构不变。
- 逻辑独立性:指用户的应用程序与数据库的逻辑结构是相互独立的。
完整性约束
- 实体完整性
- 参照完整性
- 用户定义完整性
关系代数运算符
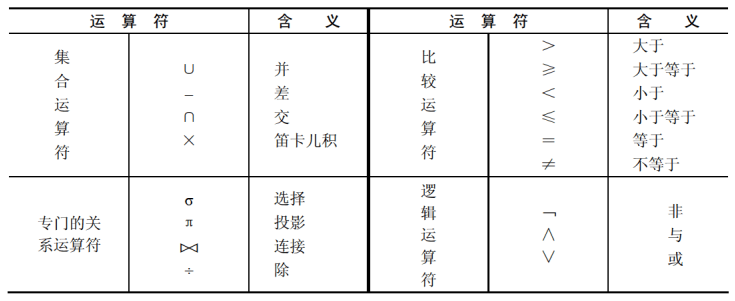
-
广义笛卡儿积(Extended Cartesian Product):两个元组分别为$n$目和$m$目的关系$R$和$S$的广义笛卡儿积是一个$(n+m)$列的元组的集合。
元组的前$n$列是关系$R$的一个元组,后$m$列是关系$S$的一个元组,记作$R \times S$,其形式定义如下:
$$ R \times S = \{ t| (t \ = \ <t^n, t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \} $$
如果$R$和$S$中有相同的属性名,可在属性名前加关系名作为限定,以示区别。若$R$有$K_1$,个元组,$S$有$K_2$个元组,则$R$和$S$的广义笛卡儿积有$K_1 \times K2$个元组。
$<t^n, t^m>$是一个元组$t^n$和$t^m$拼接成的一个元组。
-
投影(Projection):投影运算是从关系的垂直方向进行运算,在关系$R$中选出若干属性列$A$组成新的关系,记作$\pi_A (R)$,其形式定义如下:
$$ \pi_A (R) = \{ t[A]|t \in R \} $$
-
选择(Selection):选择运算是从关系的水平方向进行运算,是从关系$R$中选择满足给定条件的诸元组,记作$\sigma_F (R)$其形式定义如下:
$$ \sigma_A (R) = \{ t| (t \in R) \wedge F(t) = True \} $$
其中,$F(t)$中的运算对象可以是:
- 属性名(或列的序号);
- 常数;
- 运算符;
- 算术比较符($<, \le, >, \ge, \neq$);
- 逻辑运算符($\wedge, \vee, \neg$)。
-
连接(Join):连接运算是从两个关系$R$和$S$的笛卡儿积中选取满足条件的元组。
可以认为笛卡儿积是无条件连接,其他的连接操作认为是有条件连接。
-
$\theta$连接:从$R$与$S$的笛卡儿积中选取属性间满足一定条件的元组。记作:
$$ R \mathop{\Join}\limits_{X \theta Y} S = \{ t| (t=<t^n,t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (t^n[X] \ \theta \ t^m[Y]) \} $$
其中:
- $X \theta Y$:连接的条件;
- $\theta$:比较运算符;
- $X$和$Y$分别为$R$和$S$上度数相等且可比的属性组;
- $t^n\left[ X \right]$表示$R$中$t^n$元组的对应于属性$X$的一个分量;
- $t^m[Y]$表示$S$中$t^m$元组的对应于属性$Y$的一个分量。
$\theta$连接也可以表示为:
$$ R \mathop{\Join}\limits_{i \theta j} S = \{ t| (t=<t^n,t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (t^n[i] \ \theta \ t^m[j]) \} $$
其中,
-
$i=1,2,3,\cdots,n$;
-
$j=1,2,3,\cdots,m$;
-
$i \theta j$:
从两个关系$R$和$S$中选取$R$的第$i$列和$S$的第$j$列之间满足$\theta$运算的元组进行连接。
$\theta$连接可以由基本的关系运算笛卡儿积和选取运算导出。因此,$\theta$连接可表示为:
$$ R \mathop{\Join}\limits_{X \theta Y} S = \sigma_{X \theta Y}(R \times S) $$
或:
$$ R \mathop{\Join}\limits_{i \theta j} S = \sigma_{i \theta j}(R \times S) $$
-
等值连接:当$\theta$为“=”时,称之为等值连接,记为$R \mathop{\Join}\limits_{i = j} S$,其形式定义如下:
$$ R \mathop{\Join}\limits_{i = j} S = \{ t| (t=<t^n,t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (t^n[i] = t^m[j]) \} $$
-
$F$连接:从关系$R$和$S$的笛卡尔积中选取属性值满足某一公式$F$的元组,记为$\mathop{\Join}\limits_{F}$。
$F$是形为$F_1 \wedge F_2 \wedge \cdots \wedge F_n$的公式,每个$F_p$是形为$i \theta j$的式子。
-
自然连接:自然连接是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且在结果集中将重复属性列去掉。
若:
-
$t^n \in R$,$t^m \in S$;
-
$R$和$S$具有相同的属性组$B$,且$B=(B_1,B_2,,B_k)$;
-
假定$R$关系的属性:
$$ A_1,A_2,\cdots,A_{n-k},B_1,B_2,\cdots,B_k $$
-
$S$关系的属性:
$$ B_1,B2,\cdots,B_k,B_{k+1},B_{k+2},\cdots,B_m $$
自然连接可以记为$R \Join S$,其形式定义如下:
$$ R \Join S = \{ t| (t = <t^n, t^m>) \wedge (t^n \in R) \wedge (t^m \in S) \wedge (R.B_1 = S.B_1) \wedge (R.B_2 = S.B_2) \wedge \cdots \wedge (R.B_k = S.B_k) \} $$
-
-
-
外连接(Outer Jion):外连接运算是连接运算的扩展,可以处理由于连接运算而缺失的信息。
外连接运算有3种:
-
左外连接(Left Outer Jion,⟕):取出左侧关系中所有与右侧关系中任一元组都不匹配的元组,用空值$null$充填所有来自右侧关系的属性,构成新的元组,将其加入自然连接的结果中。
-
右外连接(Right Outer Jion,⟖):取出右侧关系中所有与左侧关系中任一元组都不匹配的元组,用空值$null$填充所有来自左侧关系的属性,构成新的元组,将其加入自然连接的结果中。
-
全外连接(Full Outer Jion,⟗)。完成左外连接和右外连接的操作。

-
SQL
-
DDL(Data Definition Language,数据定义语言):用来定义数据库对象:数据库,表,列等。
关键字:
CREATE、DROP、ALTER等。 -
DML(Data Manipulation Language,数据操作语言):用来对数据库中表的数据进行增删改。
关键字:
INSERT、DELETE、UPDATE等。 -
DQL(Data Query Language,数据查询语言):用来查询数据库中表的记录。
关键字:
SELECT等。 -
DCL(Data Control Language,数据控制语言):用来定义数据库的访问权限和安全级别,及创建用户。
授权语句格式(GRANT):
GRANT <权限>[, <权限>] ...
[ON <对象类型> <对象名>]
TO<用户>[, <用户>]...
[WITH GRANT OPTION];
常见的操作权限如下:
| 对象 | 对象类型 | 操作权限 |
|---|---|---|
| 属性列 | TABLE |
SELECT、INSERT、UPDATE、DELETE、ALL PRIVILEGES |
| 视图 | TABLE |
SELECT、INSERT、UPDATE、DELETE、ALL PRIVILEGES |
| 基本表 | TABLE |
SELECT、INSERT、UPDATE、DELETE、ALTER、INDEX、ALL PRIVILEGES |
| 数据库 | DATABASE |
CREATETAB |
- 建立表的权限,可由DBA授予普通用户;
WITH GRANT OPTION:表示获得了这些权限的用户还可以将权限赋给其他用户。
收回权限语句格式(REVOKE):
REVOKE <权限>[, <权限>]...
[ON <对象类型> <对象名>]
FROM <用户>[, <用户>];
函数依赖
| 名称 | 条件 | 结论 |
|---|---|---|
| 函数依赖 | 元组在$X$上的属性值相等,那么在$Y$上的属性值也相等 | $X$函数决定$Y$或$Y$函数依赖于$X$,记作$X \rightarrow Y$ |
| 非平凡的函数依赖 | $X \rightarrow Y$,$Y \not\subseteq X$ | $X \rightarrow Y$是非平凡的函数依赖 |
| 平凡的函数依赖 | $X \rightarrow Y$,$Y \subseteq X$ | $X \rightarrow Y$是平凡的函数依赖 |
| 完全函数依赖 | $X \rightarrow Y$,$X’ \subset X$,$X’ \not\rightarrow Y$ | $Y$对$X$完全函数依赖,记作$X \stackrel{f}{\longrightarrow} Y$ |
| 部分函数依赖(局部函数依赖) | $X \rightarrow Y$,$X \stackrel{f}{\not\longrightarrow} Y$ | $Y$对$X$部分函数依赖,记作$X \stackrel{P}{\longrightarrow} Y$ |
| 传递依赖 | $X \rightarrow Y$,$Y \not\subseteq X$,$Y \rightarrow Z$ | $Z$对$X$传递依赖 |
| 名称 | 定义 |
|---|---|
| 码(候选码,候选关键字) | 若$K \stackrel{f}{\rightarrow} U$,则$K$为$R$的候选码 |
| 主属性 | 包含在任何一个候选码中的属性 |
| 非主属性 | 不包含在任何一个候选码中的属性 |
| 外码 | $X$非$R$的码,但$X$是另一个关系的码,则称$X$为外码 |
Armstrong公理系统:
| 定律 | 条件 | F蕴含 |
|---|---|---|
| 自反律 | $Y \subseteq X \subseteq U$ | $X \rightarrow Y$ |
| 增广律 | $X \rightarrow Y$,$Z \subseteq U$ | $XZ \rightarrow XZ$ |
| 传递律 | $X \rightarrow Y,\ Y \rightarrow Z$ | $X \rightarrow Z$ |
| 规则 | 条件 | F蕴含 |
|---|---|---|
| 合并规则 | $X \rightarrow Y,\ X \rightarrow Z$ | $X \rightarrow YZ$ |
| 伪传递律 | $X \rightarrow Y,\ WY \rightarrow Z$ | $XW \rightarrow Z$ |
| 分解规则 | $X \rightarrow Y,\ Z \subseteq Y$ | $X \rightarrow Z$ |
关系模式的分解
范式
-
第一范式(1NF):若关系模式R的每一个分量是不可再分的数据项,则关系模式R属于第一范式。
如,关系模式$R<U,F>$:
$$ U = \{ 学号,姓名,学院,院长,课程号,课程名,成绩 \} \\ F = \{ 学号 \rightarrow 姓名,学号 \rightarrow 学院,学院 \rightarrow 院长,课程号 \rightarrow 课程名,(学号,课程号) \rightarrow 成绩 \} $$
-
第二范式(2NF):若关系模式$R \in 1NF$,且每一个非主属性完全依赖于码,则关系模式$R \in 2NF$。
即当1NF消除了对主键的部分函数依赖后就能满足2NF。
例如,$学号 \rightarrow 学院$,即$(学号,课程号) \stackrel{P}{\rightarrow} 学院$(部分依赖于码),所以$R \not\in 2NF$。
模式的分解需要保持函数依赖。根据$F$,将$R$分解为:
-
$R_1<U_1,F_1>$:
$$ U_1 = \{ 学号,姓名,学院,院长 \} \\ F_1 = \{ 学号 \rightarrow 姓名,学号 \rightarrow 学院,学院 \rightarrow 院长 \} $$
-
$R_2<U_2,F_2>$:
$$ U_2 = \{ 课程号,课程名 \} \\ F_2 = \{ 课程号 \rightarrow 课程名 \} $$
-
$R_3<U_3,F_3>$:
$$ U_3 = \{ 学号,课程号,成绩 \} \\ F_3 = \{ (学号,课程号) \rightarrow 成绩 \}
则,$R1 \in 2NF$,$R2 \in 2NF$,$R3 \in 2NF$。
-
-
第三范式(3NF):若关系模式$R(R \in 2NF)$中任何一个非主属性都不传递函数依赖于码。
若关系模式$R<U,F>$($U$为关系集,$F$为函数依赖集)中不存在这样的码$X$,使得:
- $X \rightarrow Y(Y \not\rightarrow X)$,
- $Y \rightarrow Z$,
则关系模式$R \in 3NF$,其中:
- $Y$为属性组,
- $Z(Z \not\subseteq Y)$为非主属性。
即当2NF消除了非主属性对主键的传递函数依赖,则称为3NF。
如,$R_1$中有$学号 \rightarrow 学院$,$学院 \rightarrow 院长$(非主属性"院长"传递依赖于主键"学号")。可将$R_1$分解为:
-
$R_{11}<U_{11},F_{11}>$:
$$ U_{11} = \{ 学号,姓名,学院 \} \\ F_{11} = \{ 学号 \rightarrow 姓名, 学号 \rightarrow 学院 \} $$
-
$R_{12}<U_{12},F_{12}>$:
$$ U_{12} = \{ 学院,院长 \} \\ F_{12} = \{ 学院 \rightarrow 院长 \} $$
范式之间的关系:
$$ 5NF \sub 4NF \sub BCNF \sub 3NF \sub 2NF \sub 1NF $$
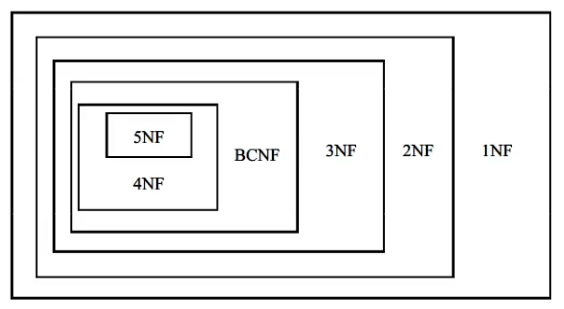
3NF和BCNE它们是进行规范化的主要目标。
1NF到4NF之间的转换关系:
| 范式 | 转换关系 |
|---|---|
| 1NF | 每一个分量是不可再分的数据项 |
| 2NF | 1NF消除了部分函数依赖后满足2NF |
| 3NF | 2NF消除了非主属性对码的传递函数依赖后满足3NF |
| BCNF | 3NF消除了主属性对码的部分和传递函数依赖后满足BCNF |
| 4NF | BCNF消除非平凡且非函数依赖的多值依赖后满足4NF |
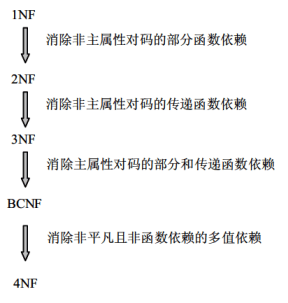
几种范式及其分解的性质:
| 性质 | 3NF | BCNF | 4NF |
|---|---|---|---|
| 消除函数依赖带来冗余 | 否 | 是 | 是 |
| 消除多值函数依赖带来冗余 | 否 | 否 | 是 |
| 保持函数依赖 | 是 | 否 | 否 |
| 保持多值函数依赖 | 否 | 否 | 否 |
数据库设计
分布式数据库
基本概念:
- 分片透明
- 复制透明
- 位置透明
- 逻辑透明
性质:
- 共享性:数据存储在不同的结点数据共享。
- 自治性:指每结点对本地数据都能独立管理。
- 可用性:指当某一场地故障时,系统可以使用其他场地上的副本而不至于使整个系统瘫痪。
- 分布性
结构化设计
跳转连接:软件设计师——结构化设计篇
模块化
-
模块:是在程序中是数据说明、可执行语句等程序对象的集合,或者是单独命名和编址的元素,例如高级语言中的过程、函数和子程序等。
在软件的体系结构中,模块是可组合、分解和更换的单元。
-
模块化:是指将一个待开发的软件分解成若干个小的简单部分一模块,每个模块可独立地开发、测试,最后组装成完整的程序。
这是一种复杂问题“分而治之”的原则。
模块化的目的是使程序的结构清晰,容易阅读、理解、测试和修改。
-
模块独立:是指每个模块完成一个相对独立的特定子功能,并且与其他模块之间的联系简单。
衡量模块独立程度的标准有(模块独立性的两个定性标准):
- 耦合性;
- 内聚性。
在将软件系统划分模块时,应尽量做到高内聚、低耦合,提高模块的独立性。
通常,可以按照在软件系统中的功能将模块分为四种类型:
- 传入模块:取得数据或输入数据,经过某些处理,再将其传送给其他模块。
- 传出模块:输出数据,在输出前可能进行某些处理。数据可能被输出到系统的外部,或者会输出到其他模块进行进一步处理。
- 变换模块:从上级调用模块得到数据,进行特定的处理,转换成其他形式,再将加工结果返回给调用模块。
- 协调模块:一般不对数据进行加工,主要是通过调用、协调和管理其他模块来完成特定的功能。
耦合和内聚

| 耦合类型 | 说明 |
|---|---|
| 无直接耦合 | 没有直接关系,不传递任何信息 |
| 数据耦合 | 调用关系,传递简单数据值 |
| 标记耦合 | 传递数据结构 |
| 控制耦合 | 调用关系,被调模块传递给主调模块控制变量 |
| 外部耦合 | 通过软件之外的环境联结 |
| 公共耦合 | 通过公共数据环境相互作用 |
| 内容耦合 | 直接使用另一个模块的内部数据 或通过非正常入口转入另一个模块内部 |

| 内聚类型 | 说明 |
|---|---|
| 偶然内聚 (巧合内聚) |
各处理之间没有任何联系 |
| 逻辑内聚 | 执行若干个逻辑上相似的功能, 通过参数确定该模块完成哪一个功能 |
| 时间内聚 | 把需要同时执行的动作组合在一起 |
| 过程内聚 | 完成多个任务,这些任务必须按指定的过程执行 |
| 通信内聚 | 所有处理都在同一个数据结构上操作, 或者各处理使用相同的输入数据或者产生相同的输出数据 |
| 顺序内聚 | 各处理都与同一功能密切相关且必须顺序执行, 前一功能元素的输出就是下一功能元素的输入 |
| 功能内聚 | 所有元素共同作用完成一个功能,缺一不可 |
系统结构设计原则
为保证总体结构设计顺利完成,应遵循以下几条原则:
-
分解——协调原则:
系统整体,具有其整体的目的和功能,但这些目的和功能的实现又是由相互联系的各个组成部分共同工作的结果。解决复杂问题的一个很重要的原则就是把它分解成多个小问题分别处理,在处理过程中根据系统总体要求协调各部门的关系。
-
自顶向下的原则:从上往下,逐层分解;先确定上层模块的功能,再确定下层模块的功能。
-
信息隐蔽、抽象的原则:上层模块只规定下层模块做什么和所属模块间的协调关系,但不规定怎么做。
-
一致性原则:统一的规范、标准、文件模式……
-
明确性原则:每个模块必须:
- 功能明确、接口明确;
- 消除多重功能和无用接口。
-
高内聚、低耦合
-
模块的扇入系数和扇出系数要合理:
- 扇出系数:模块直接调用其他模块的个数。
- 扇入系数:模块被其他模块调用时,直接调用它的模块个数。
一个设计得好的系统的平均扇入、扇出系数通常是 3 或 4,一般不应超过 7。
-
模块的规模适当:
- 过大的模块常常使系统分解得不充分;
- 过小的模块有可能降低模块的独立性,造成系统接口的复杂性。
-
模块的作用范围应该在其控制范围之内。
-
避免或减少使用病态连接:病态连接是指从中部进入或访问一个模块。
系统文档
| 人员 | 阶段 | 文档 |
|---|---|---|
| 用户 系统分析人员 |
系统规划 系统分析 |
沟通文档,主要是规划报告、合同、方案:
|
| 系统开发人员 项目管理人员 |
项目期内 | 沟通文档(项目管理文件),主要是计划、报告类文档:
|
| 系统测试人员 系统开发人员 |
测试 | 系统测试人员根据以下文档对系统进行测试:
|
| 系统开发人员 用户 |
系统运行期间 | 用户通过系统开发人员撰写的文档运行系统:
|
| 系统开发人员 系统维护人员 |
维护 | 沟通文档:
|
| 用户 维修人员 |
运维 | 用户将运行过程中的问题进行记载:
|
数据流图和数据字典
软件工程
跳转连接:软件设计师——软件工程篇
软件过程模型
能力成熟度模型(从1开始):
| 级别 | 说明 |
|---|---|
| 初始级 | 杂乱无章,几乎没有明确定义的步骤。 |
| 可重复级 | 建立基本的项目管理过程和实践来跟踪项目费用、进度和功能特性。 |
| 已定义级 | 将管理和工程文档化、标准化并综合成标准软件过程; 使用标准开发过程(或方法论)构建(或集成)系统。 |
| 己管理级 | 对软件过程和产品质量制定了的详细度量标准,且有定量的理解和控制。 |
| 优化级 | 加强了定量分析,通过过程质量和新观念、新技术使过程不断地改进。 |
能力成熟度集成连续式模型(从0开始):
| 能力等级 | 目标 |
|---|---|
| 未完成的 | 未执行或未得到等级1中的所有目标。 |
| 已执行的 | 可标识的输入工作产品到输出工作产品的转换,实现特定目标。 关注:特定目标的完成。 |
| 已管理的 | 已管理的过程的制度化。 关注:针对单个过程实例的能力。 |
| 已定义级的 | 已定义的过程的制度化。 关注:过程的组织级标准化和部署。 |
| 定量管理的 | 可定量管理的过程的制度化。 说明:使用测量和质量保证来控制和改进。 |
| 优化的 | 优化的过程的制度化。 说明:使用量化手段改变和优化。 |
各开发模型的适用范围:
| 模型 | 说明 | 适用范围 |
|---|---|---|
| 瀑布模型 | 将软件生存周期中的活动定为线性顺序链接的阶段模型 | 需求明确、大致固定且变更少 |
| V模型 | 瀑布模型的变体,强调测试贯穿项目的始终,是一种测试的开发模型 | 需求明确、低风险 |
| 增量模型 | 融合瀑布模型和原型迭代,核心功能先完成,每轮迭代都会有新的增量,核心功能得到充分测试,强调每个增量均发布一个可操作的产品 | 快速构造可运行的产品,产品升级,领域熟悉或已有原型 |
| 演化模型 | 迭代的过程模型,需求无法被完整定义,功能在使用过程中不断完善 | 对软件需求缺乏准确认识的情况 |
| 原型模型 | 原型开发方法模型,目的是快速、低成本地构建原型系统 | 需求不清或多变、领域陌生;不适合大规模系统 |
| 螺旋模型 | 结合瀑布和演化模型,强调引入风险分析,属于面向对象开发模型 | 庞大、复杂、高风险的系统,开发人员有丰富的风险评估经验和知识 |
| 喷泉模型 | 面向对象模型,特点是迭代、无间隙和支持重用,各阶段无明显界限,可迭代交叉 | 面向对象的开发过程 |
| 统一过程 | 用例驱动、以架构为中心、迭代和增量 |
统一过程模型阶段里程碑和关注点总结:
| 阶段 | 里程碑 | 关注 |
|---|---|---|
| 初始阶段 | 生命周期目标 | 项目的初创活动 |
| 精化阶段 | 生命周期架构 | 需求分析和架构演进 |
| 构建阶段 | 初始运作功能 | 系统的构建 |
| 移交阶段 | 产品发布 | 软件提交方面的工作 |
软件需求
-
功能需求:考虑系统要做什么,在何时做,在何时以及如何修改或升级。
-
性能需求:考虑软件开发的技术性指标。
例如:
- 存储容量限制;
- 执行速度;
- 响应时间;
- 吞吐量。
-
用户或人的因素:考虑用户的类型。
例如:
- 各种用户对使用计算机的熟练程度,需要接受的训练;
- 用户理解、使用系统的难度;
- 用户错误操作系统的可能性。
-
环境需求:考虑未来软件应用的环境,包括硬件和软件。
- 对硬件设备的需求包括:机型、外设、接口、地点、分布、湿度、磁场干扰等;
- 对软件的需求包括:操作系统、网络、数据库等。
-
界面需求:
考虑以下方面:
- 来自其他系统的输入;
- 到其他系统的输出;
- 对数据格式的特殊规定;
- 对数据存储介质的规定。
-
文档需求:考虑需要哪些文档,文档针对哪些读者。
-
数据需求:
考虑以下方面:
- 输入、输出数据的格式;
- 接收、发送数据的频率;
- 数据的准确性和精度;
- 数据流量;
- 数据需保持的时间。
-
资源使用需求:
考虑以下方面:
- 软件运行时所需要的数据、其他软件、内存空间等资源;
- 软件开发、维护时,所需的人力、支撑软件、开发设备。
-
安全保密要求:
考虑以下方面:
- 是否需要对访问系统或系统信息加以控制;
- 隔离用户数据的方法;
- 用户程序如何与其他程序和操作系统隔离
- 系统备份要求。
-
可靠性要求:
考虑以下方面:
- 系统的可靠性要求;
- 系统是否必须检测和隔离错误;
- 出错后,重启系统允许的时间。
-
软件成本消耗与开发进度需求:
考虑以下方面:
- 开发是否有规定的时间表;
- 软/硬件投资有无限制。
-
其他非功能性要求:
如采用某种开发模式,需要确定:
- 质量控制标准;
- 里程碑和评审;
- 验收标准;
- 各种质量要求的优先级;
- 可维护性方面的要求。
单元测试
在测试中应检查以下要点:
-
模块接口:模块的接口保证了测试模块的数据流可以正确地流入、流出。
在测试中应检查以下要点:
- 测试模块的输入参数和形式参数在个数、属性、单位上是否一致。
- 调用其他模块时,所给出的实际参数和被调用模块的形式参数在个数、属性、单位上是否一致。
- 调用标准函数时,所用的参数在属性、数目和顺序上是否正确。
- 全局变量在各模块中的定义和用法是否一致。
- 输入是否仅改变了形式参数。
- 开/关的语句是否正确。
- 规定的I/O格式是否与输入/输出语句一致。
- 在使用文件之前是否已经打开文件或使用文件之后是否己经关闭文件。
-
局部数据结构
-
重要的执行路径
-
出错处理
-
边界条件
集成测试
-
非增量集成:分别测试各个模块,再把这些模块组合起来进行整体测试。
- 优点:可以对模块进行并行测试,能充分利用人力,并加快工程进度。
- 缺点:容易混乱,出现错误不容易查找和定位。
-
增量集成:以小增量的方式逐步进行构造和测试。
增量式测试的范围一步步扩大,错误容易定位,更易于对接口进行彻底测试,并且可以运用系统化的测试方法。
增量集成策略:
- 自项向下集成测试:从主控模块(主程序)开始,以深度优先或广度优先的方式。不需要驱动模块。
- 自底向上集成测试:从原子模块开始进行构造和测试。不需要桩模块。
- 回归测试
- 冒烟测试
测试方法
黑白盒测试法属于动态测试。设计测试用例时应包括合理的输入条件和不合理的输入条件。
黑盒测试
等价类划分:从每个等价类中选取一个代表性数据作为测试用例。用少量代表性的测试用例取得较好的测试效果。
分为有效等价类和无效等价类。
定义等价类的原则如下。
- 在输入条件规定了取值范围或值的个数的情况下,可以定义1个有效等价类和2个无效等价类。
- 在输入条件规定了输入值的集合或规定了“必须如何”的条件的情况下,可以定义1个有效等价类和一个无效等价类。
- 在输入条件是一个布尔量的情况下,可以定义一个有效等价类和一个无效等价类。
- 在规定了输入数据的一组值(假定$n$个),并且程序要对每一个输入值分别处理的情况下,可以定义$n$个有效等价类和1个无效等价类。
- 在规定了输入数据必须遵守的规则的情况下,可以定义一个有效等价类(符合规则)和若干个无效等价类(从不同角度违反规则)。
- 在确知己划分的等价类中,各元素在程序处理中的方式不同的情况下,则应将该等价类进一步划分为更小的等价类。
无效等价类的划分:每个无效等价类的测试用例,只违反一个输入的取值范围。如果违反了多个输入的取值范围,那便是不好的测试用例。
例如,输入$x$的取值范围是$0 \sim 10$,输入$y$的取值范围是$-10 \sim -1$,那么可以定义三个等价类:
- 有效等价类1:$x$的取值范围是$0 \sim 10$,输入$x$的取值范围是$-10 \sim -1$;
- 无效等价类2:$x$的取值范围是$x < 0 \ \ OR \ \ x > 10$,输入$y$的取值范围是$-10 \sim -1$;
- 无效等价类3:$x$的取值范围是$0 \sim 10$,输入$x$的取值范围是$x < -10 \ \ OR \ \ x > -1$。
除了等价类划分还有:
- 边界值分析
- 错误推测
- 因果图
白盒测试
逻辑覆盖:考察用测试数据运行被测程序时,对程序逻辑的覆盖程度。
主要的逻辑覆盖标准有6种,它们的覆盖程度从低到高为:
| 逻辑覆盖 | 说明 |
|---|---|
| 语句覆盖 | 每条语句执行一次 |
| 分支(判定)覆盖 | 每个分支获得一次True/False |
| 条件覆盖 | 每个分支中的每个逻辑条件的所有可能取值满足一次 |
| 判定/条件覆盖 | 分支覆盖 + 条件覆盖 |
| 条件组合覆盖 | 每个判定中条件的各种可能值的组合都出现一次 |
| 路径覆盖 | 覆盖被测试程序中所有可能的路径 |
除了逻辑覆盖还有:
- 循环覆盖
- 基本路径测试
软件维护
正确性和完善性维护是针对来自系统内部的维护,适应性和预防性是针对来自系统外部的维护。
-
正确性维护针对的是系统内部的错误。
来自系统内部的,与错误有关的都是属于正确性维护。
-
完善性维护针对的是系统内部与功能、性能等方面有关的维护。
来自系统内部的,与系统功能、性能等方面有关的改善都是完善性维护。完善性维护的需求可以来自外部,例如功能的扩展。
-
适应性维护是针对来自系统外部的技术、管理需求等方面的变化。
针对来自系统外部的变化,系统功能等方面没有缺失,仅仅只是适应当前环境变化所做的更改,都是属于适应性维护。
-
预防性维护针对的是未来的环境变化。
沟通路径
软件项目中沟通路径$m$的计算公式(人数$n$):
-
沟通图中无主程序员时:
$$ m = \sum_{i=1}^{n} i-1 = \cfrac{(n-1)n}{2} $$
-
沟通图中有主程序员时:
$$ m = n - 1 $$
估算模型
COCOMO模型:
| 模型分类 | 类型或说明 |
|---|---|
| 基本COCOMO模型 | 静态单变量模型,对整个软件系统进行估算 |
| 中级COCOMO模型 | 静态多变量模型,将系统模型分为系统和部件2个层次 |
| 详细COCOMO模型 | 将系统模型分为系统、子系统和模块3个层次 |
| COCOMOII | 层次结构,分为应用组装模型、早期设计阶段模型和体系结构阶段模型 |
COCOMOII的使用时期及规模估算选择:
| 阶段性模型 | 规模估算选择 |
|---|---|
| 应用组装模型 | 对象点 |
| 早期设计阶段模型 | 功能点 |
| 体系结构阶段模型 | 代码行 |
甘特图和PERT图
风险分类
| 分类 | 说明 |
|---|---|
| 项目风险 | 威胁到项目计划。 风险因素: |
| 技术风险 | 威胁到软件的质量及交付时间。 风险因素: |
| 市场风险 | 开发了一个没有人真正需要的产品或系统。 |
| 策略风险 | 开发的产品不再符合公司的整体商业策略。 |
| 销售风险 | 开发了一个销售部门不知道如何去销售的产品。 |
| 管理风险 | 由于重点的转移或人员的变动而失去了高级管理层的支持。 |
| 预算风险 | 没有得到预算或人员的保证。 |
风险管理总结:
| 风险管理 | 说明 |
|---|---|
| 风险识别 | 指出对项目计划的威胁。可通过建立风险条目检查表识别。 |
| 风险预测 | 从风险发生的可能性或概率、风险产生的后果评估可能发生的风险。 |
| 风险评估 | 从风险发生的概率和产生的影响评估风险。可用定义风险参照水准技术评估。 |
| 风险控制 | 目的是辅助项目建立处理风险的策略。策略是风险避免、风险监控和RMMM计划。 |
| 风险避免 | 应对风险的最好办法是主动地避免风险。 |
| 风险监控 | 项目管理者应监控某些可以提供风险高低变化指示的因素。 |
ISO/IEC 9126 软件质量模型
由3个层次组成:
- 第一层:质量特性
- 第二层:质量子特性
- 第三层:度量指标
该模型的质量特性和质量子特性:
| 质量特性 | 质量子特性 |
|---|---|
| 功能性(Functionality) | |
| 适合性(Suitability) | |
| 准确性(Accurateness) | |
| 互用性(Interoperability) | |
| 依从性(Compliance) | |
| 安全性(Security) | |
| 可靠性(Reliability) | |
| 成熟性(Maturity) | |
| 容错性(Fault tolerance) | |
| 易恢复性(Recoverability) | |
| 易使用性(Usability) | |
| 易理解性(Understandability) | |
| 易学性(Learnability) | |
| 易操作性(Operability) | |
| 效率(Efficiency) | |
| 时间特性(Time behavior) | |
| 资源特性(Resource behavior) | |
| 可维护性(Maintainability) | |
| 易分析性(Analyzability) | |
| 易改变性(Changeability) | |
| 稳定性(Stability) | |
| 易测试性(Testability) | |
| 可移植性(Portability) | |
| 适应性(Adaptability) | |
| 易安装性(Installability) | |
| 一致性(Conformance) | |
| 易替换性(Replaceability) |
质量子特性的含义:
- 功能性:
- 适合性:与对规定任务能否提供一组功能以及这组功能是否适合有关的软件属性。
- 准确性:与能够得到正确或相符的结果或效果有关的软件属性。
- 互用性:与其他指定系统进行交互操作的能力相关的软件属性。
- 依从性:使软件服从有关的标准、约定、法规及类似规定的软件属性。
- 安全性:与避免对程序及数据的非授权故意或意外访问的能力有关的软件属性。
- 可靠性:
- 成熟性:与由软件故障引起失效的频度有关的软件属性。
- 容错性:与在软件错误或违反指定接口的情况下维持指定的性能水平的能力有关的软件属性。
- 易恢复性:与在故障发生后,重新建立其性能水平并恢复直接受影响数据的能力,以及为达到此目的所需的时间和努力有关的软件属性。
- 易使用性:
- 易理解性:与用户为理解逻辑概念及其应用所付出的劳动有关的软件属性。
- 易学性:与用户为学习其应用(例如操作控制、输入、输出)所付出的努力相关的软件属性。
- 易操作性:与用户为进行操作和操作控制所付出的努力有关的软件属性。
- 效率:
- 时间特性:与响应和处理时间以及软件执行其功能时的吞吐量有关的软件属性。
- 资源特性:与软件执行其功能时,所使用的资源量以及使用资源的持续时间有关的软件属性。
- 可维护性:
- 易分析性:与为诊断缺陷或失效原因,或为判定待修改的部分所需努力有关的软件属性。
- 易改变性:与进行修改、排错或适应环境变换所需努力有关的软件属性。
- 稳定性:与修改造成未预料效果的风险有关的软件属性。
- 易测试性:为确认经修改软件所需努力有关的软件属性。
- 可移植性:
- 适应性:与软件转移到不同环境时的处理或手段有关的软件属性。
- 易安装性:与在指定环境下安装软件所需努力有关的软件属性。
- 一致性:使软件服从与可移植性有关的标准或约定的软件属性。
- 易替换性:与一软件在该软件环境中用来替代指定的其他软件的可能和努力有关的软件属性。
计算机网络
跳转连接:软件设计师——计算机网络篇
网络分类
按通信距离分类:
| 网络分类 | 分布距离 | 计算机分布范围 | 传输速率 |
|---|---|---|---|
|
局域网
MAN |
|||
| 10m左右 | 房间 | 4Mbps ~ 1Gbps | |
| 100m左右 | 楼寓 | ||
| 1000m左右 | 校园 | ||
|
城域网
WAN |
10km | 城市 | 50Kbps ~ 100 Mbps |
|
广域网
LAN |
100km以上 | 国家或全球 | 9.6Kbps ~ 45Mbps |
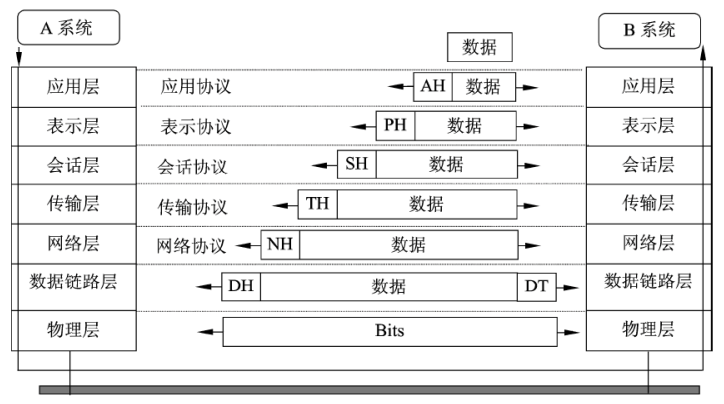
ISO/OSI 网络体系结构
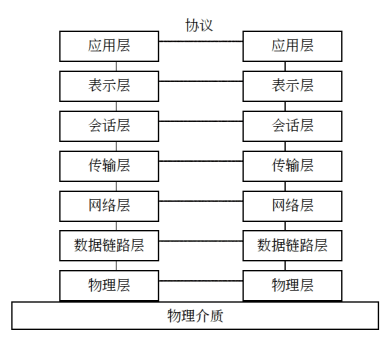
- 通信子网对应于OSI中的低三层:
- 物理层
- 数据链路层
- 网络层
- 资源子网对应于OSI中的高三层:
- 会话层
- 表示层
- 应用层
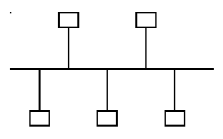
网络的拓扑结构
-
总线型结构:
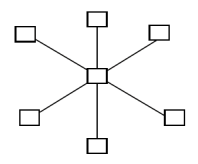
-
星型结构:
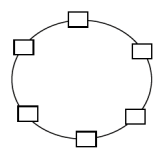
-
环型结构:
-
树型结构:
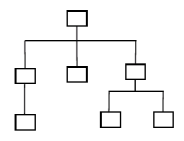
-
分布式结构:
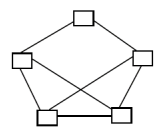
网络设备
按照ISO/OSI的分层将互连设备分类:
-
物理层设备:
- 中继器(Repeater)
- 集线器(Hub):一种多端口的中继器。集线器不能自动寻址,但可以检测发送冲突。
-
数据链路层设备:
-
网桥(Bridge)
-
交换机(Switch):一种多端口的网桥。
交换技术:
- 端口交换
- 帧交换
- 信元交换
-
-
网络层设备:路由器(Router)
-
应用层设备:网关(Gateway)
网络传输介质
- 有线介质:
- 双绞线(Twisted-Pair)
- 同轴电缆(Coaxial)
- 光纤(Fiber Optic)
- 无线介质:
- 微波
- 红外线和激光
- 卫星通信
LAN 模型
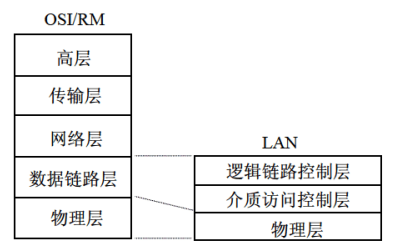
以太网
- IEEE 802.3中定义的标准局域网,速度为10Mbps,传输介质为细同轴电缆;
- IEEE 802.3u中定义的快速以太网,速度为100Mbps,传输介质为双绞线;
- IEEE 802.3z中定义的千兆以太网,速度为1000Mbps,传输介质为光纤或双绞线。
TCP/IP 协议族
基本特性:
- 逻辑编制:IP地址包括:
- 网络ID号:用来标识网络;
- 子网ID号:用来标识网络上的一个子网;
- 主机ID号:用来标识子网上的一台计算机。
- 路由选择
- 域名(DNS)解析
- 错误检测
- 流量控制
TCP/IP分层模型由4个层次构成:
- 应用层
- 传输层
- 网际层
- 网络接口层
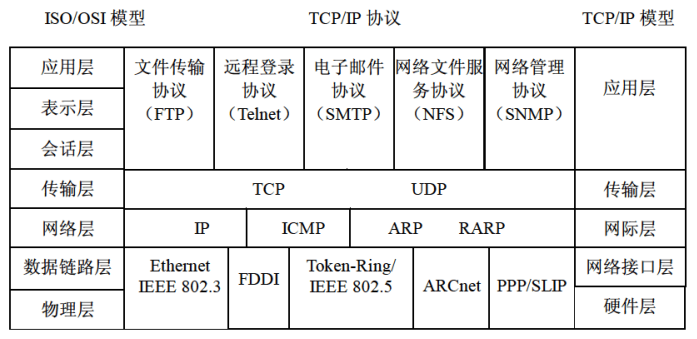
-
TCP(传输控制协议):在IP提供的不可靠数据服务的基础上为应用程序提供了可靠的、面向连接的、全双工的数据传输服务。
采用三次握手来确认建立和关闭连接是否成功。
-
UDP(用户数据报协议):一种不可靠的、无连接的协议,可以保证应用程序进程间的通信。
地址解析协议
- ARP(地址解析协议):将IP地址转换为MAC地址(物理地址)。
- RARP(反地址解析协议):将MAC地址转换为IP地址。
动态主机配置协议 DHCP
DHCP客户端可以从DHCP服务器获得以下内容:
- 本机IP地址
- DNS服务器地址
- DHCP服务器地址
- 默认网关的地址
无效地址
-
Windows无效地址:169.254.X.X
169.254.X.X是Windows系统在DHCP信息租用失败时自动给客户机分配的IP地址。
-
Linux无效地址:0.0.0.0
域名和URL
主机名.本地名.组名.最高层域名
主机所在的网络级别较高:
本地名.组名.最高层域名
URL即统一资源定位器(统一资源定位符):
协议名://主机名.域名.域名后缀.域名分类/目录/网页文件
IP
IPv4:

全0代表的是网络,全1代表的是广播。
IPv4能表示的地址个数为:
$$ 2^{32} \approx 40亿 $$

**IPv6:**长达128位的地址空间,彻底解决IPv4地址不足的问题。
IPv6理论上能表示的地址个数:
$$ 2^{128} = 3.4 \times 10^{38} $$
防火墙技术
防火墙技术是建立在内外网络边界上的过滤封锁机制,它认为:
- 内部网络是安全和可信赖的;
- 外部网络是不安全和不可信赖的。
防火墙的作用:防止不希望的、未经授权地进出被保护的内部网络。
防火墙技术经历了三个发展阶段:
- 包过滤防火墙
- 应用代理网关防火墙
- 状态检测技术防火墙
入侵检测
入侵检测系统(DS)作为防火墙之后的第二道安全屏障。
入侵检测系统有效的弥补了防火墙系统对网络上的入侵行为无法识别和检测的不足。
入侵防御系统(IPS)是在入侵检测系统的基础上发展起来的,不仅能检测到网络中的攻击行为,同时主动对攻击行为发出响应,对攻击进行防御。
网络攻击
攻击目标对于攻击者是个黑盒子。
网络攻击手段有:
- 拒绝服务攻击(Dos攻击):使计算机或网络无法提供正常的服务通过不断向计算机发起请求来实现的。
- 重放攻击:攻击者发送一个目的主机已经接受过的报文来达到攻击目的。
- 口令入侵攻击。
- 特洛伊木马。
- 端口欺骗攻击。
- 网络监听。
- IP欺骗攻击。
- SQL注入攻击。
病毒
病毒类型:
-
Worm(蠕虫病毒):
- 欢乐时光,
- 熊猫烧香,
- 红色代码,
- 爱虫病毒,
- 震网。
-
Trojan(特洛伊木马):通过内部发起连接与外部主机建立联系,由外部主机控制并盗取用户信息。
计算机感染特洛伊木马后的典型线型是有未知程序试图建立网络连接。
常见的木马如冰河。
-
Backdoor(后门病毒)。
-
Macro(宏病毒):
宏病毒感染的对象主要是文本文档、电子表格等。
算法设计与分析
跳转连接:软件设计师——算法设计与分析篇
算法设计方法
| 算法设计方法 | 说明 | 特点 | 实例 |
|---|---|---|---|
| 分治法 |
|
原问题规模大且能分解为多个与原问题相同的子问题 |
|
| 动态规划法 |
|
求解具有某种最优性质的问题 |
|
| 贪心法 | 与动态规划类似,但贪心法考虑的是局部最优解 | 并不保证得到全局最优解,但通常能得到近似最优解 |
|
| 回溯法 | 在解空间树中,按深度优先策略,从根结点出发搜索解空间树 |
|
|
| 分支限界法 | 与回溯法类似,在解空间树种按广度优先或最小耗费优先方式,搜索满足约束条件的一个解 |
|
|
算法实例
查找算法
查找算法在查找成功时的平均查找长度关键字和给定值比较次数的期望值:
$$ ASL = \sum_{i=1}^{n}{P_iC_i} $$
-
$P_i$为对表中第$i$个记录进行查找的概率,
一般认为$P_i=\cfrac{1}{n}, 1 \le i \le n$,即$\sum_{i=1}^{n}{P_i}$;
-
$C_i$为查找成功时,已经进行过比较的关键字个数。
静态查找表有以下查找方法:
- 顺序查找;
- 折半查找;
- 分块查找。
动态查找表有以下查找方法:
- 二叉排序树;
- 平衡排序树;
- B-树;
- 哈希表。
顺序查找中,$C_i$取决于所查记录在表中的位置。一般情况下,$C_i = n - i + 1$,在等概率下,顺序查找的平均查找长度为:
$$ ASL_{ss} = \cfrac{1}{n} \sum_{i=1}^{n}{(n-i+1)} = \cfrac{n+1}{2} $$
折半查找的平均查找长度(假设结点总数为$n=2^h-1$,即折半查找树为深度$h=log_2(n+1)$的满二叉树):
$$ ASL_{bs} = \cfrac{1}{n} \sum_{i=1}^{n}{i \times 2^{i-1}} = \cfrac{n+1}{n} log_2{(n+1)} - 1 $$
当$n$值较大时,$ASL_{bs} \approx log_2{(n+1)} - 1$。
哈希函数
哈希函数构造方法:
- 直接定址法;
- 数字分析法;
- 平方取中法;
- 折叠法;
- 随机数法;
- 除留余数法
哈希函数的构造要考虑到:
- 压缩性:节省存储空间;
- 散列性:尽量减少冲突。
除留取余数法:
$$ f(key)=key \enspace mod \enspace p\quad (p\le m),\ m为散列表长 $$
冲突处理方法:
- 开放地址法;
- 多重散列法(再哈希法);
- 链地址法;
- 公共溢出区法……
开放地址法(三种寻找空散列地址的方法):
-
线性探测法(线性探测再散列):
$$ H_i=(H(key)+d) mod m $$
其中:
- $d$取$0,1,2,…,m-1$;
- $m$为散列表的长度。
$d$初始为0,如果有冲突,那么$d$就通过递增来寻找空的散列地址。
-
二次探测法(二次探测再散列):
$$ H_i=(H(key)+q^2) mod m $$
其中:
- $q$取$0,1,-1,2,-2,…,\pm k$,$k \le \cfrac{m}{2}$
- $m$为散列表的长度
排序算法
排序算法有稳定排序和不稳定排序两种。假设待排序序列中,$R_i$和$R_j$值相同,且$R_i$领先于$R_j$,排序后:
- 稳定排序:排序后$R_i$和$R_j$相对次序不变,$R_i$任领先于$R_j$;
- 不稳定排序:排序后可能出现$R_j$领先于$R_i$的情况。
根据记录存储的位置可分为:
- 内部排序:待排序记录存储在内存中进行排序的过程。
- 外部排序:排序记录的数量很大,内存无法容纳全部记录,在排序过程需要对外存进行访问的排序过程。
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 | 是否归位 |
|---|---|---|---|---|---|---|
| 直接插入排序 | $O(n^2)$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 稳定 | 否 |
| 希尔排序 | $O(n^{1.3})$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 不稳定 | 否 |
| 简单选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 | 是 |
| 堆排序 | $O(nlog_2{n})$ | $O(nlog_2{n})$ | $O(nlog_2{n})$ | $O(1)$ | 不稳定 | 是 |
| 冒泡排序 | $O(n^2)$ | $O(n^2)$ | $O(n)$ | $O(1)$ | 稳定 | 是 |
| 快速排序 | $O(nlog_2{n})$ | $O(n^2)$ | $O(nlog_2{n})$ | $O(log_2{n})$ | 不稳定 | 是 |
| 归并排序 | $O(nlog_2{n})$ | $O(nlog_2{n})$ | $O(nlog_2{n})$ | $O(n)$ | 稳定 | 否 |
是否归位:在排序过程中,能否确定某些元素的最终排序位置。


评论