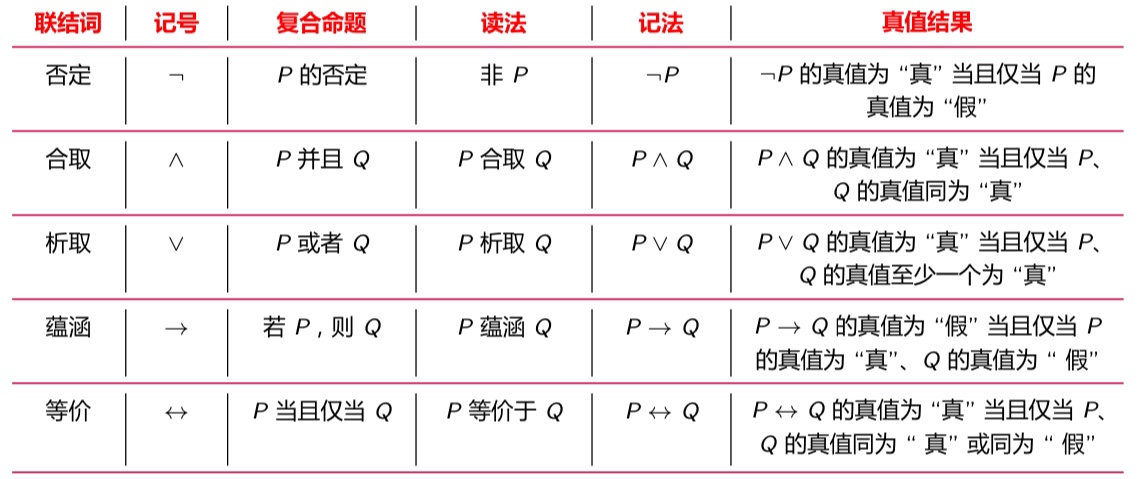
命题的定义
具有确切真值的陈述句称为命题(proposition)。命题可以取一个 “值”,称为真值。真值只有 “真”(用 “T” or “1” 表示,即 True)和 “假”(用 “F” or “0” 表示,即 False)。
通常用带或不带下标的大写英文字母表示命题。
非命题
一切没有判断内容的句子,如命令句(祈使句)、感叹句、疑问句、二义性的陈述句等都不能作为命题。
原子命题与复合命题
- 原子命题(简单命题):不能再分解为更简单命题的命题。
- 复合命题:可以分解为更为简单命题的命题。这些简单命题之间是通过联结词和标点符号复合而成。
命题变元
一个特定的命题是一个常值命题,它不是具有值 “T”,就是具有值 “F”。
一个任意的没有赋予具体内容的原子命题就是一个变量命题,常称它为命题变量(或命题变元,propositional vatiable)。
命题变元无具体的真值,它的变域是集合 ${T,F}$(或 ${0,1}$)。
联结词
联结词是两个命题真值之间的联结,而不是命题内容之间的连接,因此复合命题的真值只取决于构成它们的各简单命题的真值,而与它们的内容无关,与二者之间是否有关系无关。

否定联结词
设 $P$ 是任意一个命题,复合命题 “非 $P$”(或 “$P$ 的否定”)称为 $P$ 的否定式(negation),记作 $\neg P$,“$\neg$” 为否定联结词。
$P$ 为真当且仅当 $\neg P$ 为假。
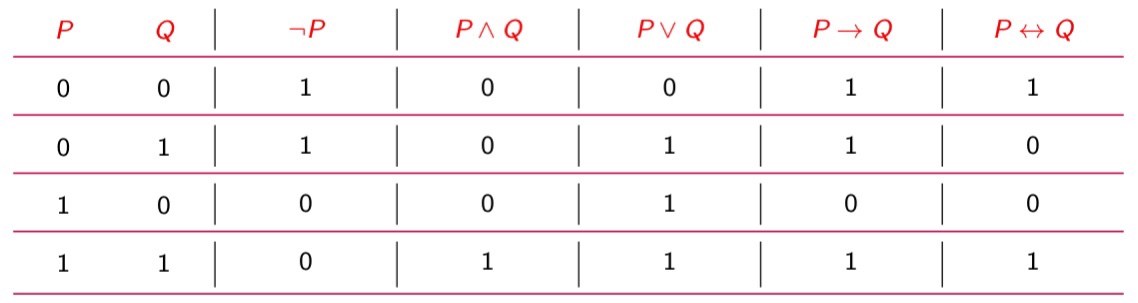
真值表:
| $P$ | $\neg P$ |
|---|---|
| 0 | 1 |
| 1 | 0 |
“$\neg$” 是自然语言中的 “非”、“不”、“没有” 等的逻辑抽象。
合取联结词
设 $P$、$Q$ 是任意两个命题,复合命题 “$P$ 并且 $Q$”(或 “$P$ 和 $Q$”)称为 $P$ 与 $Q$ 的合取式(conjunction),记作 $P \wedge Q$,“$\wedge$” 为合取联结词。
$P \wedge Q$ 为真当且仅当 $P$、$Q$ 同为真。
真值表:
| $P \qquad Q$ | $P \wedge Q$ |
|---|---|
| $0 \qquad 0$ | $0$ |
| $0 \qquad 1$ | $0$ |
| $1 \qquad 0$ | $0$ |
| $1 \qquad 1$ | $1$ |

析取联结词
设 $P$、$Q$ 是任意两个命题,复合命题 “$P$ 或 $Q$” 称为 $P$ 与 $Q$ 的析取式(disjunction),记作 $P \vee Q$,“$\vee$” 为析取联结词。
$P \vee Q$ 为真当且仅当 $P$、$Q$ 至少有一个为真。
真值表:
| $P \qquad Q$ | $P \vee Q$ |
|---|---|
| $0 \qquad 0$ | $0$ |
| $0 \qquad 1$ | $1$ |
| $1 \qquad 0$ | $1$ |
| $1 \qquad 1$ | $1$ |
联结词 “$\vee$” 是自然语言中的 “或”、“或者” 等的逻辑抽象。
自然语言中的 “或” 有 “可兼或”(或称为同或)、“不可兼或”(即异或)两种。
严格来讲,析取联结词实际上代表的是可兼或。
异或联结词
设 $P$、$Q$ 是任意两个命题,复合命题 “$P$ 或 $Q$” 有时代表不可兼或,记作 $P \oplus Q$ 或 $P \overline{\vee} Q$,“$\oplus$” 或 “$\overline{\vee}$” 为异或联结词。
$P \oplus Q$ 为真当且仅当 $P$、$Q$ 中有且仅有一个为真。
真值表:
| $P \qquad Q$ | $P \vee Q$ |
|---|---|
| $0 \qquad 0$ | $0$ |
| $0 \qquad 1$ | $1$ |
| $1 \qquad 0$ | $1$ |
| $1 \qquad 1$ | $0$ |
蕴涵联结词
设 $P$、$Q$ 是任意两个命题,复合命题 “如果 $P$,则 $Q$” 称为 $P$ 与 $Q$ 的蕴涵式(implication),记作 $P \rightarrow Q$,“$\rightarrow$” 为蕴含联结词。
$P \rightarrow Q$ 为假当且仅当 $P$ 为真且 $Q$ 为假($P$ 为假时,认为该蕴涵式为真)。
一般把蕴涵式 $P \rightarrow Q$ 中的 $P$ 称为该蕴涵式的前件,$Q$ 称为蕴涵式的后件。
真值表:
| $P \qquad Q$ | $P \vee Q$ |
|---|---|
| $0 \qquad 0$ | $1$ |
| $0 \qquad 1$ | $1$ |
| $1 \qquad 0$ | $0$ |
| $1 \qquad 1$ | $1$ |


等价联结词
设 $P$、$Q$ 是任意两个命题,复合命题 “$P$ 当且仅当 $Q$” 称为 $P$ 与 $Q$ 的蕴涵式(implication),记作 $P \leftrightarrow Q$,“$\leftrightarrow$” 为等价联结词。
$P \leftrightarrow Q$ 为真当且仅当 $P$、$Q$ 同为真假。
真值表:
| $P \qquad Q$ | $P \vee Q$ |
|---|---|
| $0 \qquad 0$ | $1$ |
| $0 \qquad 1$ | $0$ |
| $1 \qquad 0$ | $0$ |
| $1 \qquad 1$ | $1$ |
“$\leftrightarrow$” 是自然语言中的 “等价”、“充分必要条件”、“当且仅当” 等的逻辑抽象。
总结
命题联结词 “$\wedge$”、“$\vee$”、“$\leftrightarrow$” 具有对称性,而 “$\neg$”、“$\rightarrow$” 没有。
优先级
优先顺序:括号、否定、合取、析取、蕴涵、等价。同级的联结词,按出现的先后次序(从左到右)。
命题联结词的应用
联结词与开关电路
设命题 $P$:开关 $S_1$ 闭合;命题 $Q$:开关 $S_2$ 闭合。则以下电路可用复合命题表示:
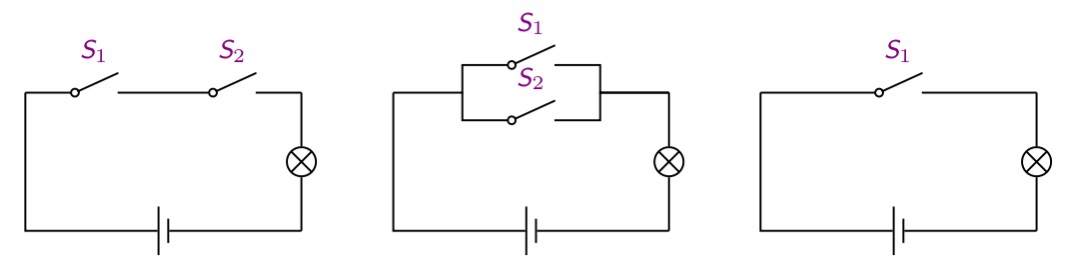
- “串联”:$P \wedge Q$;
- “并联”:$P \vee Q$;
- “断开”:$\neg P$。
联结词与逻辑电路
-
与门:$\wedge$
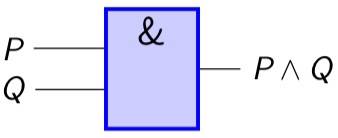
-
或门:$\vee$

-
非门:$\neg$

联结词与网页检索
在布尔检索中,
- $\wedge$(一般用 AND 表示)用于匹配包含两个检索项的记录;
- $\vee$(一般用 OR 表示)用于匹配包含两个检索项至少一个的记录;
- $\neg$(一般用 NOT 表示)用于排除某个特定的检索项。
联结词与位运算
- 按位与:$\wedge$;
- 按位或:$\vee$;
- 按位取反:$\neg$。
命题公式
复合命题是由原子命题与联结词构成的命题。所以,当其中的原子命题是命题变元时,此复合命题也即为命题变元的函数,且该函数的值仍为 “真” 或 “假” 值,这样的函数可形象地称为 “真值函数” 或 “命题公式”,此命题公式没有确切的真值。
命题公式的定义
命题演算的合式公式(Well Formed Formula,WFF),又称命题公式(简称公式),按如下规则生成:
- 命题变元本身是一个公式;
- 如果 $G$ 是公式,则 $(\neg G)$ 也是公式;
- 如果 $G$、$H$ 是公式,则 $(G \wedge H)$、$(G \vee H)$、$(G \rightarrow H)$、$(G \leftrightarrow H)$ 也是公式;
- 仅由有限步使用规则 1、2、3 后所得到的包含命题变元、联结词和括号的符号串才是命题公式。
如果 $G$ 是含有 $n$ 个命题变元 $P_1、P_2、P_3、\cdots、P_n$ 的公式,可记为:$G(P_1,P_2,P_3,\cdots,P_n)$ 或简写为 $G$。
- 原子命题变元是最简单的合式公式,称为原子合式公式,简称原子公式;
- 命题公式没有真值,只有对其命题变元进行真值指派后,方可确定命题公式的真值;
- 整个公式的最外层括号可以省略,公式中不影响运算次序的括号也可以省略;
- 在实际应用中,为了便于存储和运算,命题公式常用二元数方式来表达。

命题公式的解释
设 $P_1、P_2、P_3、\cdots、P_n$ 是出现在公式 $G$ 中的所有命题变元,给 $P_1、P_2、P_3、\cdots、P_n$ 指定一组真值,则这组真值称为 $G$ 的一个解释,常记为 $I$。
- 如果公式 $G$ 在解释 $I$ 下是真的,则称 $I$ 满足 $G$,此时 $I$ 是 $G$ 的成真赋值;
- 如果 $G$ 在解释 $I$ 下是假的,则称 $I$ 弄假于 $G$,此时 $I$ 是 $G$ 的成假赋值。
命题公式的分类
- 永真公式(又叫重言式,tautology):如果在它的所有解释之下其真值都为 “真”。
- 永假公式(又叫矛盾式,contradiction):如果在它的所有解释下其真值都为 “假”。
- 不可满足公式:即永假公式。
- 可满足公式(satisfiable):不为永假公式的公式。
- $G$ 是永真的当且仅当 $\neg G$ 是永假的;
- $G$ 是可满足的当且仅当至少有一个解释 $I$,使 $G$ 在 $I$ 下为真;
- 若 $G$ 是永真式,则 $G$ 一定是可满足式,但反之可满足式不一定是永真式。
等价的命题公式
设 $G$、$H$ 是两个命题公式,$P_1、P_2、P_3、\cdots、P_n$ 是出现在 $G$、$H$ 中所有的命题变元,如果对于 $P_1、P_2、P_3、\cdots、P_n$ 的 $2^n$ 个解释,$G$ 与 $H$ 的真值结果都相同,则称公式 $G$ 与 $H$ 是等价的,记作 $G = H$(或 $G \Leftrightarrow H$)。
公式等价的充分必要条件
对于任意两个公式 $G$ 和 $H$,$G = H$ 的充分必要条件是公式 $G \leftrightarrow H$ 是永真公式。
Proof:
- 必要性:假定 $G = H$,则 $G$、$H$ 在其任意解释 $I$ 下或同为真或同为假,于是由 “$\leftrightarrow$” 的意义知,公式 $G \leftrightarrow H$ 在其任何的解释 $I$ 下,其真值为 “真”,即 $G \leftrightarrow H$ 为永真公式。
- 充分性:假定公式 $G \leftrightarrow H$ 是永真公式,$I$ 是它的任意解释,在 $I$ 下,$G \leftrightarrow H$ 为真,因此,$G$,$H$ 或同为真或同为假,由于 $I$ 的任意性,故有 $G = H$。
可判定性:能否给出一个可行方法,完成对任意公式的判定问题(类型或等价判定)。
命题公式是可判定的。
命题公式的基本等价关系
设 $G$、$H$、$S$ 为任意的命题公式。
| 性质 | 等式 |
|---|---|
| 幂等律 | $G \vee G = G$ $G \wedge G = G$ |
| 交换律 | $G \vee H = H \vee G$ $G \wedge H = H \wedge G$ |
| 结合律 | $G \vee (H \vee S) = (G \vee H) \vee S$ $G \wedge (H \wedge S) = (G \wedge H) \wedge S$ |
| 同一律 | $G \wedge 0 = G$ $G \vee 1 = G$ |
| 零律 | $G \vee 1 = 1$ $G \wedge 0 = 0$ |
| 分配律 | $G \vee (H \wedge S) = (G \vee H) \wedge (G \vee S)$$G \wedge (H \vee S) = (G \wedge H) \vee (G \wedge S)$ |
| 吸收率 | $G \vee (G \wedge H) = G$ $G \wedge (G \vee H) = G$ |
| 矛盾律 | $\neg G \wedge G = 0$ |
| 排中律 | $\neg G \vee G = 1$ |
| 双重否定律 | $\neg(\neg G) = G$ |
| 德摩根律 | $\neg(G \vee H) = \neg G \wedge \neg H$$\neg(G \wedge H) = \neg G \vee \neg H$ |
| 蕴涵式 | $G \rightarrow H = \neg G \vee H$ |
| 假言易位 | $G \rightarrow H = \neg H \rightarrow \neg G$ |
| 等价式 | $G \leftrightarrow H = (G \rightarrow H) \wedge (H \rightarrow G) = (\neg G \vee H) \wedge (\neg H \vee G)$ |
| 等价否定等式 | $G \leftrightarrow H = \neg G \leftrightarrow \neg H$ |
| 归谬论 | $(G \rightarrow H) \wedge (G \rightarrow \neg H) = \neg G$ |
基本等价关系的应用
(1)判断公式类型

(2)证明公式等价

(3)开关电路化简
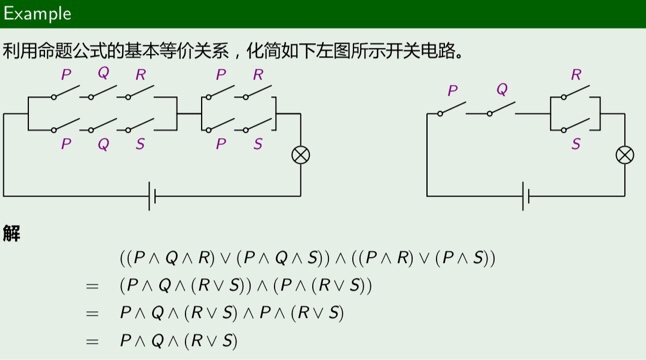
(4)逻辑电路化简
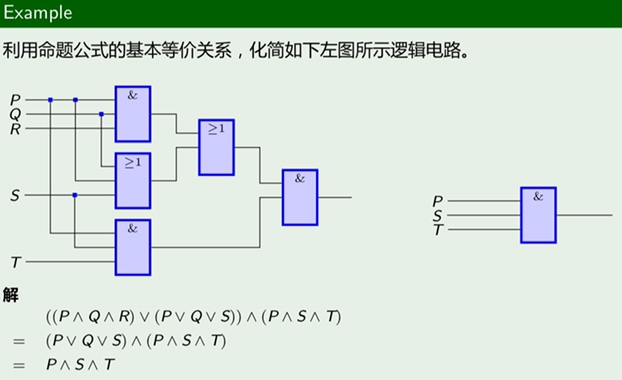
(5)其他
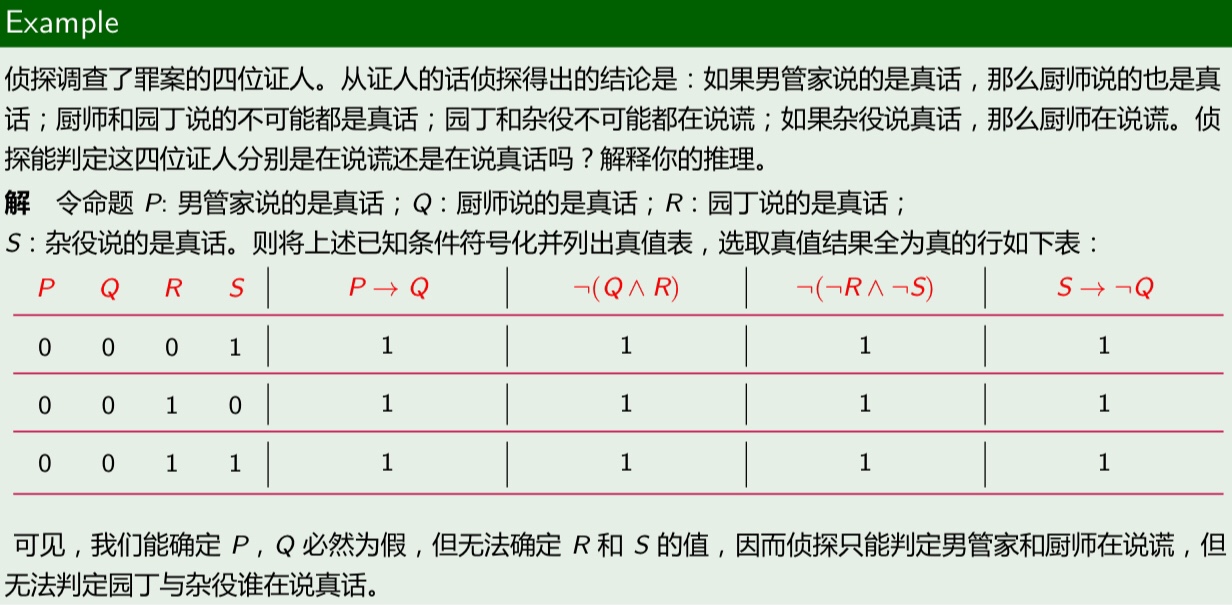
范式
- 命题变元或命题变元的否定称为文字。
- 有限个文字($\ge 1$)的析取称为简单析取式(或子句)。 单个文字可构成子句。
- 有限个文字($\ge 1$)的合取称为简单合取式(或短语)。 单个文字可构成短语。
- $P$ 与 $\neg P$ 称为互补对。
- 有限个($\ge 1$)简单合取式(短语)的析取式称为析取范式(disjunctive normal form)。
- 有限个($\ge 1$)简单析取式(子句)的合取式称为合取范式(conjunctive normal form)。
文字可以是子句、短语、析取范式、合取范式。

- 命题公式的析取范式可以指出公式何时为真,而合取范式可以指出公式何时为假,从而能够替代真值表。
- 命题公式的范式表达并不唯一。
Example:
-
$P$、$\neg P$ 可以是文字、短语、子句、析取范式、合取范式。
-
$P \vee Q \vee \neg R$ 是子句、合取范式、析取范式。
-
将该式认为是子句,那么单个子句就可构成合取范式。
-
将 $P$、$Q$、$\neg R$ 认为是短语,那么三个短语析取可构成析取范式。
-
$(P \vee Q \vee \neg R)$ 是子句、合取范式。
加了括号后该式就被认为是一个整体,不能作为析取范式。
-
-
$\neg P \wedge Q \wedge R$ 是短语、析取范式、合取范式。
- 将该式认为是短语,那么单个短语就可构成析取范式。
- 将 $\neg P$、$Q$、$R$ 认为是子句,那么三个子句合取可构成合取范式。
- $(\neg P \wedge Q \wedge R)$ 是短语、析取范式。
-
$P \vee (Q \vee \neg R)$ 即不是析取范式也不是合取范式,但转换为 $P \vee Q \vee \neg R$ 后,即是析取范式又是合取范式。
范式存在定理
联结词之间可以通过命题公式的基本等价关系进行相互转换,因此可以通过逻辑等价公式求出等价的析取范式和合取范式,具体步骤如下:
- 将公式中的 $\rightarrow$、$\leftrightarrow$ 用联结词 $\neg$、$\wedge$、$\vee$ 来取代(使用蕴涵式和等价式)。
- 将否定联结词移到各个命题变元的前端,并消去多余的否定号(使用双重否定律和德摩根律)。
- 利用分配律,可将公式化成一些合取式的析取,或化成一些析取式的合取。
对任意一个公式,经过以上步骤(期间可用其他等价公式来化简),必能化成与其等价的析取范式和合取范式。

主范式
范式是不唯一的,对构成范式的子句或短语进一步进行规范化,形成唯一的主析取范式和主合取范式。
极大项和极小项
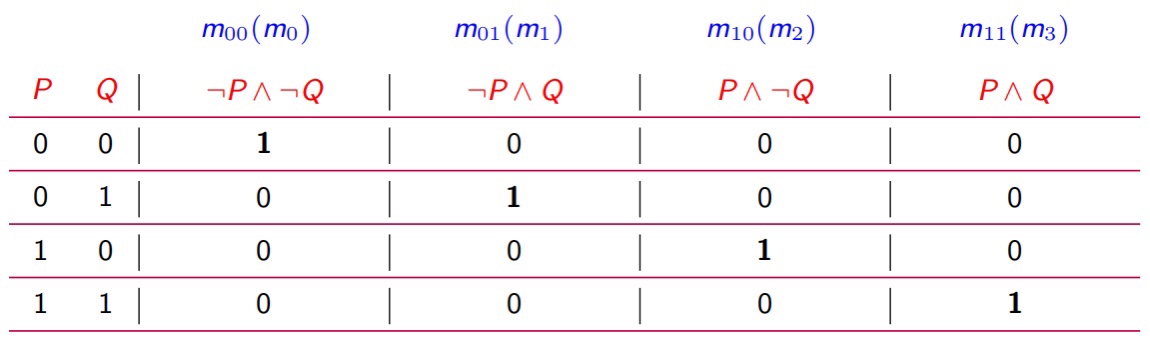
在含有 $n$ 个命题变元 $P_1、P_2、P_3、\cdots、P_n$ 的短语或子句中,若 每个命题变元与其否定不同时存在,但二者之一恰好出现一次且仅一次,并且出现的次序与 $P_1、P_2、P_3、\cdots、P_n$ 一致,则
- 称此短语为关于 $P_1、P_2、P_3、\cdots、P_n$ 的一个极小项,
- 称此子句为关于 $P_1、P_2、P_3、\cdots、P_n$ 的一个极大项。
若有 $n$ 个命题,则应有 $2^n$ 个不同的极小项和 $2^n$ 个不同的极大项。
对于极小项:
- 没有两个不同的极小项是等价的。
- 每个极小项只有一组成假赋值,因此可用于给极大项编码。 编码规则为:命题变元与 0 对应,命题变元的否定与 1 对应。
Example:
设命题变元 $P$、$Q$,
对于极大项(与极小项相反的规定):
- 没有两个不同的极大项是等价的。
- 每个极大项只有一组成假赋值,因此可用于给极大项编码。 编码规则为:命题变元与 0 对应,命题变元的否定与 1 对应。
Example:
设命题变元 $P$、$Q$,

极小项的编码可对应为真情况时,相应的短语为真的真值序列。极大项的编码可对应为假情况时,相应的子句为假的真值序列。
极小项和极大项还有以下性质:
设有 $n$ 个命题变元,设 $i,j \in {0, 1, \cdots, 2^{n-1}}$ 且 $i \neq j$,$m_i、m_j$ 代表这 $n$ 个命题变元对应的极小项,$M_i、M_j$ 代表对应的命题变元的极大项。那么就有
-
$m_i \wedge m_j = 0$,
$M_i \vee M_j = 1$;
-
$m_i = \neg M_i$,
$M_i = \neg m_i$;
-
$\displaystyle \bigvee_{i=0}^{2^n-1}{m_i} = 1$,
$\displaystyle \bigwedge_{i=0}^{2^n-1}{M_i} = 0$。
主析取范式和主合取范式
- 在给定的析取范式中,若每一个短语都是极小项,且按照编码从小到大的顺序排列,则称该范式为主析取范式(principal disjunctive normal form)。
- 在给定的合取范式中,若每一个子句都是极大项,且按照编码从小到大的顺序排列,则称该范式为主合取范式(principal conjunctive normal form)。
如果一个主析取范式不包含任何极小项,则称该主析取范式为 “空”;如果一个主合取范式不包含任何极大项,则称主合取范式为 “空”。
任何一个公式都有与之等价的主析取范式和主合取范式。
- 如果某一公式的主析取范式包含所有的极小项,即主合取范式为空,则该公式为永真公式。
- 如果某一公式主合取范式包含所有的极大项,即主析取范式为空,则该公式为永假公式。
- 若有两个公式,它们具有相同的主析取范式或主合取范式,则两公式等价。
主范式求解定理
-
求出该公式所对应的析取范式和合取范式。
-
消去重复出现的命题变元,矛盾式或重言式。
-
若析取(合取)范式的某一个短语(子句)$B_i$ 中缺少命题变元 $P$,则可用如下方式将 $P$ 补进去:
- 求主析取范式:$B_i = B_i \wedge 1 = B_i \wedge (\neg P \vee P) = (B_i \wedge \neg P) \vee (B_i \wedge P)$;
- 求主合取范式:$B_i = B_i \vee 0 = B_i \vee (\neg P \wedge P) = (B_i \vee \neg P) \wedge (B_i \vee P)$。
主析取范式的极小项编码序列与主合取范式的极大项变编码序列是互补的。因此,只需求出主析取范式或主合取范式中其中之一,就可对应求出主合取范式或主析取范式。
公式转换法


真值表技术
从真值表按所给的算法求出主范式的方法,称为真值表技术 (technique of truth table)。
方法:
- 列出真值表,选出公式的真值结果为真的所有的行,在这样的每一行中,找到其每一个解释所对应的极小项,将这些极小项进行析取即可得到相应的主析取范式。
- 列出真值表,选出公式的真值结果为假的所有的行,在这样的每一行中,找到其每一个解释所对应的极大项,将这些极大项进行合取即可得到相应的主合取范式。
推理
推理是指从一组前提合乎逻辑的推出结论的思维过程。
基本推理形式
设 $G_1、G_2、\cdots、G_n、H$ 是命题公式,称 $H$ 是 $G_1、G_2、\cdots、G_n$ 的逻辑结果当且仅当对任意解释 $I$,如果 $I$ 使得 $G_1 \wedge G_2 \wedge \cdots \wedge G_n$ 为真,则 $I$ 也会使 $H$ 为真,记为 $G_1、G_2、\cdots、G_n\ \Rightarrow\ H$,“$\Rightarrow$” 称为蕴涵关系,此时称 $G_1、G_2、\cdots、G_n\ \Rightarrow\ H$ 为有效的,否则称为无效的。
$G_1、G_2、\cdots、G_n$ 称为一组前提,有时用集合 $\Gamma$ 来表示,记为 $\Gamma = {G_1,G_2,\cdots,G_n}$,$H$ 称为结论。此时也称 $H$ 是前提集合 $\Gamma$ 的逻辑结果,记为 $\Gamma \Rightarrow H$。
推理的判定定理
公式 $H$ 是前提集合 $\Gamma = {G_1,G_2,\cdots,G_n}$ 的逻辑结果当且仅当 $(G_1 \wedge G_2 \wedge \cdots \wedge G_n) \rightarrow H$ 为永真公式。
判定方法:
- 真值表技术,
- 公式转换法,
- 主析取范式法。

基本蕴涵关系
设 $G$、$H$、$I$ 为任意命题公式。
| 规则 | 公式 |
|---|---|
| 简化规则 | $G \wedge H \Rightarrow G$ $G \wedge H \Rightarrow H$ |
| 添加规则 | $G \Rightarrow G \vee H$ |
| 合取引入规则 | $G,H \Rightarrow G \wedge H$ |
| 选言三段论 | $G \vee H, \neg G \Rightarrow H$ |
| 假言推理规则 | $G \rightarrow H, G \Rightarrow H$ |
| 否定后件式 | $G \rightarrow H, \neg H \Rightarrow \neg G$ |
| 假言三段论 | $G \rightarrow H, H \rightarrow I \Rightarrow G \rightarrow I$ |
| 二难推论 | $G \vee H, G \rightarrow I, H \rightarrow I \Rightarrow I$ |
![])(16265520749814.jpg)
自然演绎法推理
-
规则 $\mathbf{P}$(称为前提引用规则):在推导过程中,可随时引入前提集合中的任意一个前提,引入附加前提时需作声明。
-
规则 $\mathbf{T}$(称为逻辑结果引用规则):在推导过程中,可随时引入公式 $S$,该公式 $S$ 是由其前的一个或多个公式(可以是前提条件或推导出来的公式)推导出来的逻辑结果。
-
规则 $\mathbf{CP}$(称为附加前提规则):如果能从给定的前提集合 $\Gamma$ 与公式 $P$ 推导出 $S$,则能从此前提集合 $\Gamma$ 推导出 $P \rightarrow S$。
原理:$P \rightarrow (Q \rightarrow R) = (P \wedge Q) \rightarrow R$。 使用场合:当结论公式是蕴涵式或析取式时使用。
命题演算推理系统 = 三个推理规则 + 基本等价公式 + 基本蕴涵公式。
从前提集合 $\Gamma$ 推出结论 $H$ 的一个演绎是构造命题公式的一个有限序列:
$$ H_1, H_2, H_3, \cdots, H_{n-1}, H_n $$
其中,$H_i$ 或者是 $\Gamma$ 中的某个前提,或者是前面的某些 $H_j(j < i)$ 的有效结论,并且 $H_n$ 就是 $H$,则称公式 $H$ 为该演绎的有效结论,或者称从前提 $\Gamma$ 能够演绎出结论 $H$ 来。
直接证明法

规则 CP 证明法

间接证明法
间接证明法又叫反证法、归谬法。
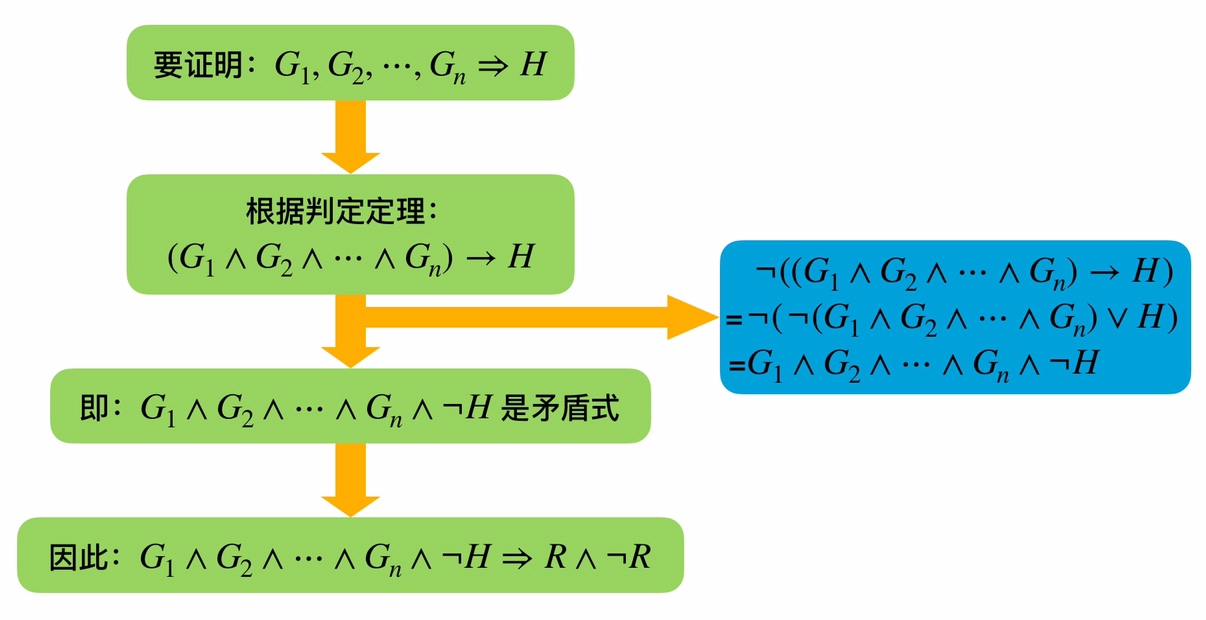

反证法在逻辑推理中有时十分方便。反证法实际上是规则 CP 的一种变形,所以可以使用 CP 证明法来代替它。
谓词逻辑
对简单命题进行分解,利用个体词、谓词和量词来描述简单命题句子,从而研究其中的逻辑关系,并研究个体与总体的内在联系和数量关系。
个体词
在原子命题中,可以独立存在的客体(句子中的主语、宾语等),称为个体词。
个体词可分为个体常量和个体变量,均在个体域内取值。
- 表示具体或特定的个体词称为个体常量。一般用带或不带下标的小写英文字母 $a, b, c, \cdots, a_1, b_1, c_1, \cdots$ 等表示。
- 表示抽象的或泛指的个体词称为个体变量。一般用带或不带下标的小写英文字母 $x, y, z, \cdots, x_1, y_1, z_1, \cdots$ 等表示。
- 个体词的取值范围称为个体域(或论域),常用 $D$ 表示。
- 宇宙间的所有个体域聚集在一起所构成的个体域称为全总个体域。无特别说明时,默认使用全总个体域。
谓词
在原子命题中,用以刻划客体的性质或客体之间的关系即是谓词。
设 $D$ 为非空的个体域,定义在 $D^n$ 上取值为 ${0,1}$ 上的 $n$ 元函数,称为 $n$ 元命题函数或 $n$ 元谓词,记为 $P(x_1, x_2, \cdots, x_n)$。其中,个体变量 $x_1, x_2, \cdots, x_n \in D$。
- 表示具体性质或关系的谓词称为谓词常量。
- 表示抽象的或泛指的性质或关系的谓词称为谓词变量。
谓词均使用大写英文字母 $P, Q, R, \cdots, F, G, H, \cdots$ 来表示。
$D^n$ 表示 $n$ 个个体都在个体域 $D$ 上取值。
- 谓词中个体词的顺序不能随意变更。
- 一元谓词用以描述某一个个体的某种特性,而 $n$ 元谓词($n \ge 2$)则用以描述 $n$ 个个体之间的关系。
- 谓词 $P(x_1, x_2, \cdots, x_n)$ 包含了个体变量,因而本身并不是命题,只有用谓词常量取代 $P$,用个体常量取代 $x_1, x_2, \cdots, x_n$ 后才会称为命题。
- 一般将没有任何个体变量的谓词称为 0 元谓词(如,$F(a_1, a_2, \cdots, a_n$)。当 $F$ 为谓词常量时,0 元谓词就成为命题。命题逻辑中的所有命题都可以表示成 0 元谓词。

量词
- 全称量词($\forall x$):所有的 $x$;任意的 $x$;一切的 $x$;每一个 $x$;……
- 存在量词($\exists x$):有些 $x$;至少有一个 $x$;某一些 $x$;存在 $x$;……
其中的 $x$ 称为作用变量。一般将其量词加在其谓词之前,记为 $(\forall x)F(x)$、$(\exists x)F(x)$。此时,$F(x)$ 称为全称量词和存在量词的辖域。
![16267650196113.jpg]
引入更准确的表达方式:以上符号化必须要特别注明个体域,在表达比较复杂的命题时会容易混淆。

其中,$T(x)$、$C(x)$、$H(x)$ 和 $N(x)$ 分别是各自个体变量的个性谓词。
统一一个全总个体域,而对每一个句子中个体变量的变化范围用一元特性谓词刻划之。这种特性谓词在加入到命题函数中时必定遵循如下原则:
- 对于全称量词($\forall x$),刻划其对应个体域的特性谓词作为蕴涵式的前件加入。
- 对于存在量词($\exists x$),刻划其对应个体域的特性谓词作为合取式的合取项加入。
谓词逻辑的真值
- $(\forall x)G(x)$:对 $\forall x \in D$,$G(x)$ 都成立。
- $(\forall x)G(x)$ 取值为 1 当且仅当对任意 $x \in D$,$G(x)$ 都取值为 1;
- $(\forall x)G(x)$ 取值为 0 当且仅当存在 $x_0 \in D$,使得 $G(x_0)$ 取值为 0。
- $(\exists x)G(x)$:存在一个 $x_0 \in D$(是有一个的意思,即可以存在一个以上,且包括一个),使得 $G(x_0)$ 成立。
- $(\exists x)G(x)$ 取值为 1 当且仅当存在 $x_0 \in D$,使得 $G(x_0)$ 取值为 1;
- $(\exists x)G(x)$ 取值为 0 当且仅当对任意 $x \in D$,$G(x)$ 都取值为 0。

当个体域 $D = {x_0, x_1, \cdots, x_n}$ 是有限集合时,
- $(\forall x)G(x) = G(x_0) \wedge G(x_1) \wedge \cdots \wedge G(x_n)$;
- $(\exists x)G(x) = G(x_0) \vee G(x_1) \vee \cdots \vee G(x_n)$。
注意:量词对变元的约束往往与量词的次序有关。不同的量词次序,可以产生不同的真值。因此当多个量词同时出现时,不能随意颠倒它们的顺序,否则会改变原有的含义。
谓词合式公式
在基于谓词的形式化中,将使用如下四种符号:
- 常量符号:指所属个体域 $D$ 中的某个元素,用带或不带下标的小写英文字母 $a, b, c, \cdots, a_1, b_1, c_1, \cdots$ 来表示。
- 变量符号:指所属个体域 $D$ 中的任意元素,用带或不带下标的小写英文字母 $x, y, z, \cdots, x_1, y_1, z_1, \cdots$ 来表示。
- 函数符号:$n$ 元函数符号 $f(x_1, x_2, \cdots, x_n)$ 可以是所属个体域集合 $D^n \rightarrow D$ 的任意一个函数,用带或不带下标的小写英文字母 $f, g, h, \cdots, f_1, g_1, h_1, \cdots$ 来表示。
- 谓词符号:$n$ 元谓词符号 $P(x_1, x_2, \cdots, x_n)$ 可以是所属个体域集合 $D_n \rightarrow {0, 1}$ 的任意一个谓词,用带或不带下标的大写英文字母 $P, Q, R, \cdots, P_1, Q_1, R_1, \cdots$ 来表示。
函数可用于表达个体词之间的转换关系,可以更方便地表示谓词逻辑中的个体词。

$n$ 元函数是个体域集合 $D^n$ 到 $D$ 的映射。
项的定义
谓词逻辑中的项(Term),被递归地定义为:
- 任意的常量符号或任意的变量符号是项。
- 若 $f(x_1, x_2, \cdots, x_n)$ 是 $n$ 元函数符号,$t_1, t_2, \cdots, t_n$ 是项,则 $f(t_1, t_2, \cdots, t_n)$ 是项。
- 仅由有限次使用以上两个规则产生的符号串才是项。
合式公式的定义
若 $P(x_1, x_2, \cdots, x_n)$ 是 $n$ 元谓词, $t_1, t_2, \cdots, t_n$ 是项,则称 $P(t_1, t_2, \cdots, t_n)$ 为原子谓词公式,简称原子公式。
满足下列条件的表达式,称为合式公式(well-formed formulae/wff),简称公式。
- 原子公式是合式公式。
- 若 $G$、$H$ 是合式公式,则 $(\neg G), (\neg H), (G \vee H), (G \wedge H), (G \rightarrow H), (G \leftrightarrow H)$ 也是合式公式。
- 若 $G$ 是合式公式,$x$ 是个体变量,则 $(\forall x)G$、$(\exists x)G$ 也是合式公式。
- 由有限次使用以上三个规则产生的表达式是合式公式。
- 公式的最外层括号可省略。
- 量词后面的括号省略方式为:一个量词的辖域中仅出现一个原子公式,则此辖域的外层括号可省略,否则不能省略。
- 一个个体词只能接受一个量词的约束,否则就是没有意义的。
自由变元与约束变元
给定一个合式公式 $G$,若变元 $x$ 出现在使用变元的量词的辖域之内,则称变元 $x$ 的出现为约束出现,此时的变元 $x$ 称为约束变元。若 $x$ 的出现不是约束出现,则称它为自由出现,此时的变元 $x$ 称为自由变元。
- 若量词后有括号,则括号内的子公式就是该量词的辖域;
- 若量词后无括号,则与量词邻接的子公式为该量词的辖域。

为了区分同一公式中,变量符号相同但不是同为自由变元或约束变元的符号(这样的变量是不同的变量,仅是符号相同),可以分别使用不同的变量符号来表示。
-
约束变元的命名规则:
- 将量词中的变元以及该量词辖域中此变量的所有约束出现都用新的个体变元替换;
- 新的变元一定要有别于改名辖域中的其他变量。
-
自由变元的命名规则:
-
将公式中出现该自由变元的每一处都用新的个体变元替换;
-
新的变元不允许在源公式中以任何约束形式出现。
也可用个体常量代入。但是代入个体常量后,公式的含义就发生了变化,即公式从具有普遍意义变为仅针对该个体变量有意义。
-
闭式
设 $G$ 是任意一个公式,若 $G$ 中无自由出现的个体变元,则称 $G$ 为封闭的合式公式,简称闭式。
闭式是一个命题。
谓词逻辑公式的解释
谓词逻辑中,公式 $G$ 的每一个解释 $I$ 由如下四部分组成:
- 非空的个体域集合 $D$。
- $G$ 中的每个常量符号,指定 $D$ 中的某个特定元素。
- $G$ 中的每个 $n$ 元函数符号,指定 $D^n$ 到 $D$ 中的某个特定的函数。
- $G$ 中的每个 $n$ 元谓词符号,指定 $D^n$ 到 ${0,1}$ 中的某个特定的谓词。
规定:公式中无自由变元,或将自由变元看成是常量符号。

谓词公式的分类
-
如果公式 $G$ 在它所有的解释下都取值为真,则称 $G$ 为有效公式。
如 $(\forall x)(\forall y)(P(x, y) \wedge Q(x, y) \rightarrow P(x, y))$。
-
如果公式 $G$ 在它所有的解释下都取值为假,则称 $G$ 为矛盾公式。
如,$(\forall x)(\forall y)(\neg P(x, y) \wedge P(x, y))$。
-
如果至少有一种解释使得公式 $G$ 取值为真,则称 $G$ 为可满足公式。
谓词公式的可判定性
-
一般情况下,谓词逻辑是不可判定的。
-
只含有一元谓词变项的公式是可判定的。
-
如下形式的公式:
$(\forall x_1) (\forall x_2) \cdots (\forall x_n) P(x_1, x_2, \cdots, x_n)$,
$(\exists x_1) (\exists x_2) \cdots (\exists x_n) P(x_1, x_2, \cdots, x_n)$。
若 $P$ 中无量词和其他自由变元时,是可判定的。
-
个体域有穷时的谓词公式是可判定的。
谓词公式的等价关系
如果公式 $G \leftrightarrow H$ 是有效公式,则公式 $G$、$H$ 称为等价的,记为 $G=H$。
设 $G(P_1, P_2, \cdots, P_n)$ 是命题演算1中的命题公式,$P_1, P_2, \cdots, P_n$ 是出现在 $G$ 中的命题变元,当用任意的谓词公式 $G_i(1\le i \le n)$ 分别代入 $P_i$ 后,得到的新谓词公式 $G(G_1, G_2, \cdots, G_n)$ 称为原公式的代入实例。
定理:永真公式的任意一个代入实例必为有效公式。
##谓词演算中的基本等价公式
命题演算中的基本等价公式在谓词演算中依然成立。
| 性质 | 等式 |
|---|---|
| 改名规则 | (\exists x)G(x) = (\exists y)G(y)(\forall x)G(x) = (\forall y)G(y) |
| 量词转换律 or 量词否定等价式 |
\neg (\exists x)G(x) = (\forall x)G(x)\neg (\forall x) \neg G(x) = (\exists x) \neg G(x) |
-
命题公式、范式和推理都是针对命题演算,它们的对象都是命题。 ↩︎


评论